
【题目】如图,已知二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
(1)求线段![]() 的长度:
的长度:
(2)若点![]() 在抛物线上,点
在抛物线上,点![]() 位于第二象限,过
位于第二象限,过![]() 作
作![]() ,垂足为
,垂足为![]() .已知
.已知![]() ,求点
,求点![]() 的坐标.
的坐标.
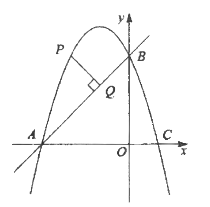
【答案】(1)AC=4
(2)P(-1,4)或(-2,3).
【解析】
(1)求出B点坐标,再利用OA=OB求出A点坐标,代入二次函数求出解析式,再令y=0即可求出与x轴的交点坐标,进而即可解题;(2)作PF∥x轴于F,利用∠BAO=45°,证明三角形PQF是等腰直角三角形,求出PF=2,再设出P,F的坐标,代入直线解析式求解方程即可解题.
解:(1)由![]() 可知二次函数与y轴的交点为B(0,3)
可知二次函数与y轴的交点为B(0,3)
∵OA=OB,
∴A(-3,0),
将A点代入二次函数解析式得:b=-2,即二次函数解析式为![]() ,
,
令y=0,即![]() 解得:x1=-3,x2=1,
解得:x1=-3,x2=1,
∴C(1,0)
∴AC=4,
(2)过点P作PF∥x轴于F,
由A,B坐标可得直线AB的解析式为y=x+3,
∴∠BAO=45°,
又∵![]() , PF∥x轴
, PF∥x轴
∴三角形PQF是等腰直角三角形,
设P(a,b),
∵P在抛物线上,
∴b=-a2-2a+3,
∵![]()
∴PF=2(勾股定理),
∴F(a+2, -a2-2a+3)
将F代入y=x+3,即-a2-2a+3=a+5,
解得a1=-1,a2=-2,
∴P(-1,4)或(-2,3).


科目:初中数学 来源: 题型:
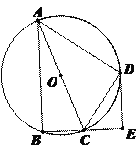
【题目】如图,四边形ABCD是⊙O的内接四边形, ![]() ,AC为直径, DE⊥BC,垂足为E.
,AC为直径, DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
(1)求反比例函数的表达式;
(2)根据图象直接写出﹣![]() x>
x>![]() 的解集;
的解集;
(3)将直线l1:y=- ![]() x沿y向上平移后的直线l2与反比例函数y=
x沿y向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
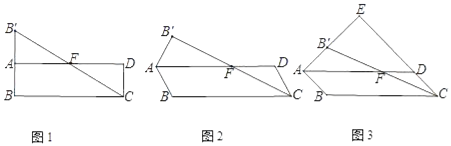
【题目】在ABCD中,点B关于AD的对称点为B′,连接AB′,CB′,CB′交AD于F点.
(1)如图1,∠ABC=90°,求证:F为CB′的中点;
(2)小宇通过观察、实验、提出猜想:如图2,在点B绕点A旋转的过程中,点F始终为CB′的中点.小宇把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:过点B′作B′G∥CD交AD于G点,只需证三角形全等;
想法2:连接BB′交AD于H点,只需证H为BB′的中点;
想法3:连接BB′,BF,只需证∠B′BC=90°.
…
请你参考上面的想法,证明F为CB′的中点.(一种方法即可)
(3)如图3,当∠ABC=135°时,AB′,CD的延长线相交于点E,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
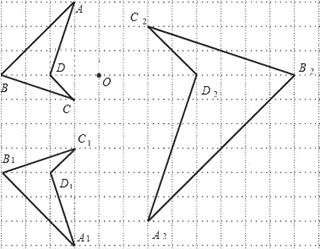
(1)图形ABCD与图形A1B1C1D1关于直线MN成轴对称,请在图中画出对称轴并标注上相应字母M、N;
(2)以图中O点为位似中心,将图形ABCD放大,得到放大后的图形A2B2C2D2,则图形ABCD与图形A2B2C2D2的对应边的比是多少(注:只要写出对应边的比即可);
(3)求图形A2B2C2D2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
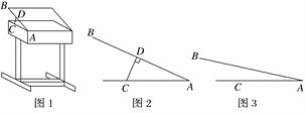
【题目】某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30 cm.
(1)如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长;
(2)如图3,当∠BAC=12°时,求AD的长.(结果保留根号)
(参考数据:sin 24°≈0.40,cos 24°≈0.91,tan 24°≈0.46,sin 12°≈0.20)
查看答案和解析>>
科目:初中数学 来源: 题型:
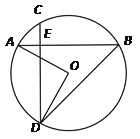
【题目】如图,在⊙O中,弦AB=弦CD,AB⊥CD于点E,且AE<EB,CE<ED,连结AO,DO,BD.
(1)求证:EB=ED.
(2)若AO=6,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
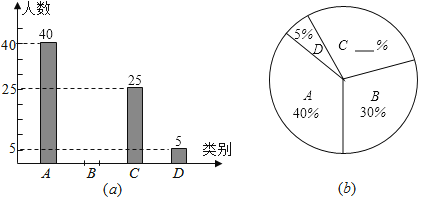
【题目】为了了解某区2018年初中毕业生毕业后的去向,某区教育部门对部分初三学生进行了抽样调查,就初三学生的四种去向(A,读普通高中;B,读职业高中;C,直接进入社会就业;D,其它)进行数据统计,并绘制了两幅不完整的统计图(a)、(b).请问:
(1)此次共调查了多少名初中毕业生?
(2)将两幅统计图中不完整的部分补充完整;
(3)若某区2018年初三毕业生共有3500人,请估计2019年初三毕业生中读普通高中的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
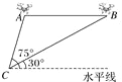
【题目】某兴趣小组借助无人飞机航拍,如图,无人飞机从A处飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为3米/秒,则这架无人飞机的飞行高度为(结果保留根号)__________米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com