
【题目】在平行四边形ABCD中,E为边上一点,连结AE并延长交直线DC于F,且CE=CF.
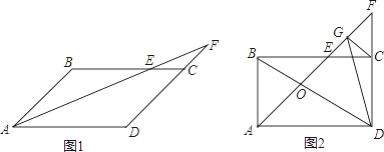
(1)如图1,求证:AF是∠BAD的平分线;
(2)如图2,若∠ABC=90°,点G是线段EF上一点,连接DG、BD、CG,若∠BDG=45°,求证:CG=![]() EF.
EF.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据四边形ABCD是平行四边形得出,AB∥DF,BC∥AD,得出∠2=∠F,∠1=∠3,进而求出∠1=∠2即可;
(2)根据∠ABC=90°,G是EF的中点可直接求得.
证明:(1)在平行四边形ABCD中,∠AEB=∠EAD
∵CE=CF,
∴∠CEF=∠CFE
∴∠AEB=∠CFE
∴∠BAF=∠DAF
∴AF是∠BAD的平分线
(2)连接BG,
∵在平行四边形ABCD中,∠ABC=90°,
∴四边形ABCD是矩形,
∵CE=CF,∠BCD=∠ECF=90°,
∴△CEF为直角三角形,
∴∠CEF=45°
∴∠BAE=45°,
∴∠EAB=45°,
∵∠BDG=45°,
∴ABGD四点共圆 (同弦BG)
又四边形ABCD是矩形
∴ABCD四点共圆
即ABGCD五点共圆
∴∠ECG=45°,
∵△CEF为直角三角形,∠ECG=45°,
∴CG是RT△CEF斜边EF上的中线,
∴CG=![]() EF.
EF.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
(1)实践操作:![]() 中,
中,![]() ,
,![]() 为直线
为直线![]() 上一点,过
上一点,过![]() 点作
点作![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,如图①,图②,图③所示,则
,如图①,图②,图③所示,则![]() 的形状为______.
的形状为______.
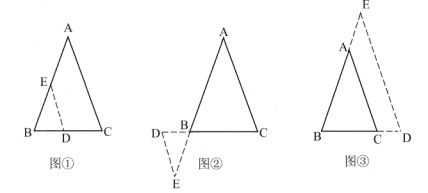
(2)问题解决:等腰三角形是一种特殊的三角形,常与全等三角形的相关知识结合在一起解决问题.如图④,![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() ,
,![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() .
.
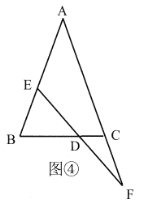
(3)拓展与应用,在(2)的条件下,如图⑤,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,若
,若![]() ,则
,则![]() 的长为______.
的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题解决)
一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?
小明通过观察、分析、思考,形成了如下思路:
思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;
思路二:将△APB绕点B顺时针旋转90°,得到△CP'B,连接PP′,求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.
(类比探究)
如图2,若点P是正方形ABCD外一点,PA=3,PB=1,PC=![]() ,求∠APB的度数.
,求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,![]() 和
和![]() 均为等边三角形,点A,D,E在同一直线上,连接BE.
均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:①![]() 的度数为 ;
的度数为 ;
②线段AD,BE之间的数量关系为 .
(2)拓展探究:如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点A,D,E在同一直线上,CM为
,点A,D,E在同一直线上,CM为![]() 中DE边上的高,连接BE,求
中DE边上的高,连接BE,求![]() 的度数,并说明理由.
的度数,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:
如图①,△ABC 和△AED 都是等腰直角三角形,∠BAC=∠EAD=90°,点 B 在线段AE 上,点 C 在线段AD 上,请直接写出线段 BE 与线段 CD 的数量与位置关系是关系: ;
(2)操作探究:
如图②,将图①中的△ABC 绕点 A 顺时针旋转α(0°<α<360°),(1)小题中线段 BE 与线段 CD 的关系是否成立?如果不成立,说明理由,如果成立,请你结合图②给出的情形进行证明;
(3)解决问题:
将图①中的△ABC 绕点 A 顺时针旋转α(0°<α<360°),若 DE=2AC,在旋转的过程中,当以 A、B、C、D 四点为顶点的四边形是平行四边形时,在备用图中画出其中的一个情形,并写出此时旋转角α的度数是 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
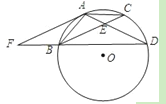
【题目】如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=![]() ED,延长DB到点F,使FB=
ED,延长DB到点F,使FB=![]() BD,连接AF.
BD,连接AF.
(1)证明:△BDE∽△FDA;
(2)试判断直线AF与⊙O的位置关系,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,每个小正方形网格的边长为1,![]() 和
和![]() 关于点
关于点![]() 成中心对称.
成中心对称.
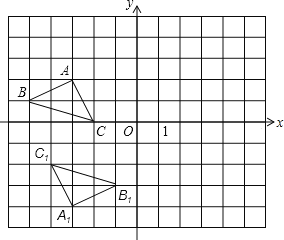
(1)画出对称中心![]() ,并写出点
,并写出点![]() 的坐标______.
的坐标______.
(2)画出![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后的
后的![]() ;连接
;连接![]() ,可求得线段
,可求得线段![]() 长为______.
长为______.
(3)画出![]() 与关于点
与关于点![]() 成中心对称的
成中心对称的![]() ;连接
;连接![]() 、
、![]() ,则四边形
,则四边形![]() 是______;(填属于哪一种特殊四边形),它的面积是______.
是______;(填属于哪一种特殊四边形),它的面积是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com