
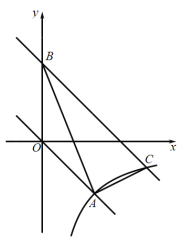
【题目】如图,在平面坐标系中,正比例函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像都经过点
的图像都经过点![]() .
.
(1)分别求出这两个函数的解析式;
(2)将直线OA向上平移3个单位后与![]() 轴交于点B,与反比例函数的图像在第四象限内的交点为C,连接
轴交于点B,与反比例函数的图像在第四象限内的交点为C,连接![]() ,求
,求![]() 的面积
的面积
(3)在(2)的条件下,反比例![]() 函数的图像上是否存在点D使得
函数的图像上是否存在点D使得![]() ?若存在直接写出点D的坐标;若不存在,请说明理由.
?若存在直接写出点D的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)6;(3)存在,D
;(2)6;(3)存在,D![]() .
.
【解析】
(1)将点![]() 代入求得k,m即可;
代入求得k,m即可;
(2)由题意的平移后直线解析式,即可得B点坐标,联立方程组求解可得第四象限内的交点C的坐标,可将△ABC的面积转化为△OBC的面积.
(3)如图,过点C作![]() 交x轴于点E,交双曲线于点D,过点C作CN⊥x轴于点N,设直线BC与x轴交点为M,求出CE的解析式,然后解方程组
交x轴于点E,交双曲线于点D,过点C作CN⊥x轴于点N,设直线BC与x轴交点为M,求出CE的解析式,然后解方程组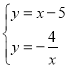 ,继而可求得答案.
,继而可求得答案.
(1)根据题意得:将![]() 代入
代入![]() 得:
得:![]() ,
,
解得:![]() ,
,
所以解析式为![]() ,
,
将![]() 代入
代入![]() 得
得![]() ,
,
解得:![]() ,
,
所以反比例函数解析式得:![]() .
.
(2)直线![]() 向上平移3个单位后解析式为
向上平移3个单位后解析式为![]() ,
,
则点B的坐标为![]() ,
,
联立解析式得:
解得![]() 或
或![]() ,
,
所以第四象限内交点C的坐标为![]() ,
,
![]() ,
,
![]() .
.
(3)存在,
如图,过点C作![]() 交x轴于点E,交双曲线于点D,过点C作CN⊥x轴于点N,设直线BC与x轴交点为M,
交x轴于点E,交双曲线于点D,过点C作CN⊥x轴于点N,设直线BC与x轴交点为M,
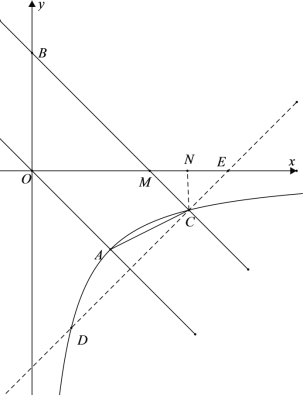
∵BC:y=-x+3交x轴于点M,∴M(3,0),
又∵B(0,3),
∴OB=OM,∠BMO=45°,
∴∠CME=∠BMO=45°,
又∵∠MCE=90°,
∴CM=CE,
∴MN=EN,
又∵C(4,-1),
∴MN=1,
∴ME=2,
∴OE=5,
∴E(5,0),
设CE解析式为:y=kx+b,
则有![]() ,
,
∴![]() ,
,
∴y=x-5,
解方程组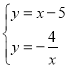 ,
,
得: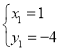 ,
,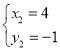 ,
,
∵C(4,-1),
∴D(1,-4).


科目:初中数学 来源: 题型:
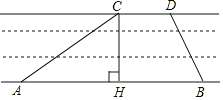
【题目】京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量出AB=180m,CD=60m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某地区企业信息化发展水平,从该地区中随机抽取50家企业调研,针对体现企业信息化发展水平的A和B两项指标进行评估,获得了它们的成绩(十分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.A项指标成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
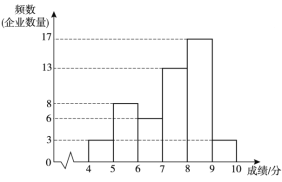
b.A项指标成绩在![]() 这一组的是:
这一组的是:
7.2 7.3 7.5 7.67 7.7 7.71 7.75 7.82 7.86 7.9 7.92 7.93 7.97
c.![]() 两项指标成绩的平均数、中位数、众数如下:
两项指标成绩的平均数、中位数、众数如下:
平均数 | 中位数 | 众数 | |
A项指标成绩 | 7.37 | m | 8.2 |
B项指标成绩 | 7.21 | 7.3 | 8 |
根据以上信息,回答下列问题:
(1)写出表中m的值
(2)在此次调研评估中,某企业A项指标成绩和B项指标成绩都是7.5分,该企业成绩排名更靠前的指标是______________(填“A”或“B”),理由是_____________;
(3)如果该地区有500家企业,估计A项指标成绩超过7.68分的企业数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个![]() 奖品和2个
奖品和2个![]() 奖品共需120元;购买5个
奖品共需120元;购买5个![]() 奖品和4个
奖品和4个![]() 奖品共需210元.
奖品共需210元.
(1)求![]() ,
,![]() 两种奖品的单价;
两种奖品的单价;
(2)学校准备在获奖的2名男生3名女生中选两名同学参加县上的比赛,请问选中两名选手都是女孩的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
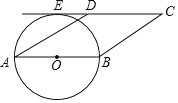
【题目】如图,在平行四边形ABCD中,AD=4,∠C=30°,⊙O与AD相交于点F,AB为⊙O的直径,⊙O与CD的延长线相切于点E,则劣弧FE的长为_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师将“校园诗词大赛”所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图,部分信息如下:
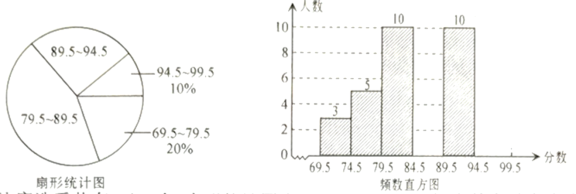
(1)本次比赛选手共有_ 人,扇形统计图中“![]() ”这一组人数占总参赛人数的百分比为_ ,频数直方图中“
”这一组人数占总参赛人数的百分比为_ ,频数直方图中“![]() ”这一组的人数为__ ;
”这一组的人数为__ ;
(2)赛前规定,成绩由高到低前![]() 的参赛选手获奖某参赛选手的比赛成绩为
的参赛选手获奖某参赛选手的比赛成绩为![]() 分,试判断他能否获奖,并说明理由;
分,试判断他能否获奖,并说明理由;
(3)成绩前四名是![]() 名男生和
名男生和![]() 名女生,若从他们中任选
名女生,若从他们中任选![]() 人作为全区“诗词大会”重点培训对象,试求恰好选中
人作为全区“诗词大会”重点培训对象,试求恰好选中![]() 男
男![]() 女的概率.
女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com