练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】为了测量校园里水平地面上的一棵大树的高度，数学综合实践活动小组的同学们开展如下活动：某一时刻，测得身高1.6m的小明在阳光下的影长是1.2m，在同一时刻测得这棵大树的影长是3.6m，则此树的高度是m．

    【答案】4.8
    【解析】解：设此树的高度是hm，则 = ，解得h=4.8（m）． 所以答案是：4.8．
    【考点精析】本题主要考查了相似三角形的应用和平行投影的相关知识点，需要掌握测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解；太阳光线可以看成是平行光线，平行光线所形成的投影称为平行投影；作物体的平行投影：由于平行投影的光线是平行的，而物体的顶端与影子的顶端确定的直线就是光线，故根据另一物体的顶端可作出其影子才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校为了解学生对“A：古诗词，B：国画，C：京剧，D：书法”等中国传统文化项目的最喜爱情况，在全校范围内随机抽取部分学生进行问卷调查（每人限选一项），并将调查结果绘制成如下不完整的统计图．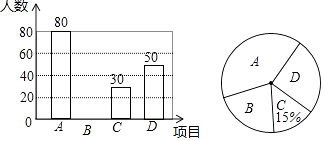

    请结合统计图回答下列问题：
    （1）在这次调查中，一共调查了名学生；在扇形统计图中，项目B对应扇形的圆心角是度；
    （2）如果该校共有2000名学生，请估计该校最喜爱项目A的学生有多少人？
    （3）若该校在A、B、C、D四项中任选两项成立课外兴趣小组，请用画树状图（或列表）计算恰好选中项目A和D的概率．
    故答案为：200，72；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

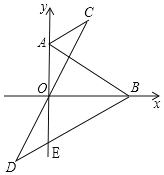
    【题目】在平面直角坐标系中，点A（0，6），B（8，0），AB=10，如图作∠DBO=∠ABO，∠CAy=∠BAO，BD交y轴于点E，直线DO交AC于点C．

    （1）①求证：△ACO≌△EDO；②求出线段AC、BD的位置关系和数量关系；

    （2）动点P从A出发，沿A﹣O﹣B路线运动，速度为1，到B点处停止运动；动点Q从B出发，沿B﹣O﹣A运动，速度为2，到A点处停止运动．二者同时开始运动，都要到达相应的终点才能停止．在某时刻，作PE⊥CD于点E，QF⊥CD于点F．问两动点运动多长时间时△OPE与△OQF全等？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：如果两个等腰三角形的顶角互补，顶角的顶点又是同一个点，而且它们的腰也分别相等，则称这两个三角形互为“顶补等腰三角形”．

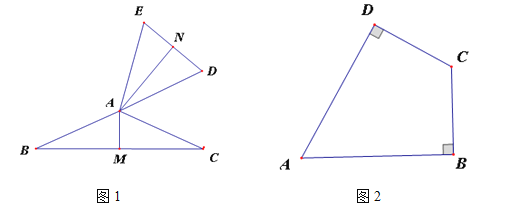
    （1）如图1，若△ABC与△ADE互为“顶补等腰三角形”．∠BAC＞90°，AM⊥BC于M，AN⊥ED于N．求证：DE=2AM；

    （2）如图2，在四边形ABCD中，AD=AB，CD=BC，∠B=90°，∠A=60°，在四边形ABCD的内部是否存在点P，使得△PAD与△PBC互为“顶补等腰三角形”？若存在，请给予证明，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图, 已知∠1＋∠2＝180o, ∠3＝∠B, 试说明∠DEC＋∠C＝180o. 请完成下列填空：

    解：∵∠1＋∠2＝180o（已知）

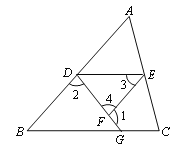
    又∵∠1＋ ＝180o（平角定义）

    ∴∠2＝ （同角的补角相等）

    ∴ （内错角相等，两直线平行）

    ∴∠3 ＝ （两直线平行，内错角相等）

    又∵∠3＝∠B（已知）

    ∴ （等量代换）

    ∴ ∥ （ ）

    ∴∠DEC＋∠C＝180o（ ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】首都国际机场连续五年排名全球最繁忙机场第二位，该机场2012﹣2016年客流量统计结果如表：

    年份

    2012

    2013

    2014

    2015

    2016

    客流量（万人次）

    8192

    8371

    8613

    8994

    9400

    根据统计表中提供的信息，预估首都国际机场2017年客流量约万人次，你的预估理由是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=20°,则∠AOB等于(　　).

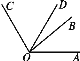
    A. 50° B. 40° C. 30° D. 20°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形ABCD中，点E是对角线AC上的动点（与点A，C不重合），连接BE．
    （1）将射线BE绕点B顺时针旋转45°，交直线AC于点F．
    ①依题意补全图1；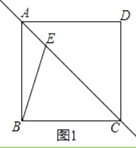

    ②小研通过观察、实验，发现线段AE，FC，EF存在以下数量关系：
    AE与FC的平方和等于EF的平方．小研把这个猜想与同学们进行交流，通过讨论，形成证明该猜想的几种想法：
    想法1：将线段BF绕点B逆时针旋转90°，得到线段BM，要证AE，FC，EF的关系，只需证AE，AM，EM的关系．
    想法2：将△ABE沿BE翻折，得到△NBE，要证AE，FC，EF的关系，只需证EN，FN，EF的关系．
    …
    请你参考上面的想法，用等式表示线段AE，FC，EF的数量关系并证明；（一种方法即可）
    （2）如图2，若将直线BE绕点B顺时针旋转135°，交直线AC于点F．小研完成作图后，发现直线AC上存在三条线段（不添加辅助线）满足：其中两条线段的平方和等于第三条线段的平方，请直接用等式表示这三条线段的数量关系．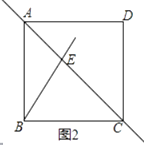

    查看答案和解析>>

    科目：初中数学 来源： 题型：

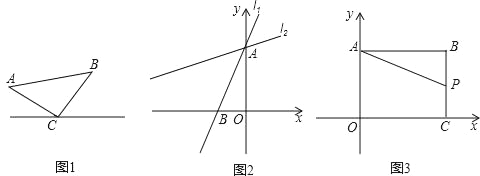
    【题目】建立模型：如图1，已知△ABC，AC=BC，∠C=90°，顶点C在直线l上．

    实践操作：过点A作AD⊥l于点D，过点B作BE⊥l于点E，求证：△CAD≌△BCE．

    模型应用：（1）如图2，在直角坐标系中，直线l1：y=x+4与y轴交于点A，与x轴交于点B，将直线l1绕着点A顺时针旋转45°得到l2．求l2的函数表达式．

    （2）如图3，在直角坐标系中，点B（8，6），作BA⊥y轴于点A，作BC⊥x轴于点C，P是线段BC上的一个动点，点Q（a，2a﹣6）位于第一象限内．问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形，若能，请求出此时a的值，若不能，请说明理由．

    查看答案和解析>>

    同步练习册答案