Question

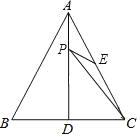
【题目】如图，在△ ABC 中，∠BAC=120°，AB=AC=4，AD⊥BC，延长AD至点E，使得AE=2AD，连接BE.

（1）求证：△ ABE 为等边三角形；

（2）将一块含 60°角的直角三角板 PMN 如图放置，其中点 P 与点 E 重合，且∠NEM=60°，边 NE 与 AB 交于点 G，边 ME 与 AC 交于点 F. 求证：BG=AF。

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）先证明∠ABD=90°-∠BAE=30°，可知AB=2AD，由因为AE=2AD，所以AB=AE，从而可知△ABE是等边三角形．
（2）由（1）可知：∠ABE=∠AEB=60°，AE=BE，然后求证△BEG≌△AEF即可得出BG=AF；

证明：（1）∵AB=AC，AD⊥BC，

∴ ∠ABD=90°-∠BAE=30°，∴ AB=2AD，

∵ AE=2AD，∴ AB=AE，

∵ ∠BAE=60°，∴△ABE 是等边三角形．

（2）∵ △ABE 是等边三角形，

∴ ∠ABE=∠AEB=60°，AE=BE①，

由（1）∠CAE=60°，∴ ∠ABE=∠CAE②，

∵ ∠NEM=∠BEA=60°，∴ ∠NEM-∠AEN=∠BEA-∠AEN，

∴ ∠AEF=∠BEG③，

由①②③得： △BEG≌△AEF（ASA）

∴ BG=AF.