
分析 (1)先变形得到x(2x-5)-2(2x-5)=0,然后利用因式分解法解方程;
(2)先把方程化为x2-7x-1=0,然后利用求根公式法解方程.
解答 解:(1)x(2x-5)-2(2x-5)=0,
(2x-5)(x-2)=0,
2x-5=0或x-2=0,
所以x1=$\frac{5}{2}$,x2=2;
(2)x2-7x-1=0,
△=(-7)2-4×1×(-1)=53,
x=$\frac{7±\sqrt{53}}{2×1}$,
所以x1=$\frac{7+\sqrt{53}}{2}$,x2=$\frac{7-\sqrt{53}}{2}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了公式法解一元二次方程.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:初中数学 来源: 题型:解答题
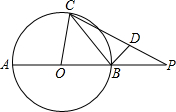 如图,AB是⊙O的直径,延长AB至P,使BP=OB,BD垂直于弦BC,垂足为点B,点D在PC上.设∠PCB=α,∠POC=2β.求证:tanα•tanβ=$\frac{1}{3}$.
如图,AB是⊙O的直径,延长AB至P,使BP=OB,BD垂直于弦BC,垂足为点B,点D在PC上.设∠PCB=α,∠POC=2β.求证:tanα•tanβ=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
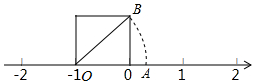 如图所示,认真观察,探讨下列问题:
如图所示,认真观察,探讨下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com