
【题目】如图,∠AOB=90°,OM平分∠AOB,将直角三角板的顶点P在射线OM上移动,两直角边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.

【答案】PC与PD相等.
【解析】
先过点P作PE⊥OA于点E,PF⊥OB于点F,构造全等三角形:Rt△PCE和Rt△PDF,这两个三角形已具备两个条件:90°的角以及PE=PF,只需再证∠EPC=∠FPD,根据已知,两个角都等于90°减去∠CPF,那么三角形全等就可证.
PC与PD相等.理由如下:
过点P作PE⊥OA于点E,PF⊥OB于点F.
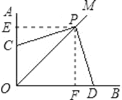
∵OM平分∠AOB,点P在OM上,PE⊥OA,PF⊥OB,
∴PE=PF(角平分线上的点到角两边的距离相等)
又∵∠AOB=90°,∠PEO=∠PFO=90°,
∴四边形OEPF为矩形,
∴∠EPF=90°,
∴∠EPC+∠CPF=90°,
又∵∠CPD=90°,
∴∠CPF+∠FPD=90°,
∴∠EPC=∠FPD=90°-∠CPF.
在△PCE与△PDF中,
∵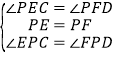 ,
,
∴△PCE≌△PDF(ASA),
∴PC=PD.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
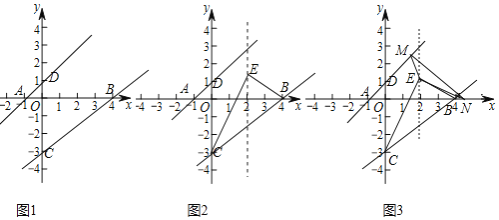
【题目】如图1,点A、B、C在坐标轴上,且A、B、C的坐标分别为![]() 、
、![]() 、
、![]() 过点A的直线AD与y轴正半轴交于点D,
过点A的直线AD与y轴正半轴交于点D,![]()
![]() 求直线AD和BC的解析式;
求直线AD和BC的解析式;
![]() 如图2,点E在直线
如图2,点E在直线![]() 上且在直线BC上方,当
上且在直线BC上方,当![]() 的面积为6时,求E点坐标;
的面积为6时,求E点坐标;
![]() 在
在![]() 的条件下,如图3,动点M在直线AD上,动点N在x轴上,连接ME、NE、MN,当
的条件下,如图3,动点M在直线AD上,动点N在x轴上,连接ME、NE、MN,当![]() 周长最小时,求
周长最小时,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
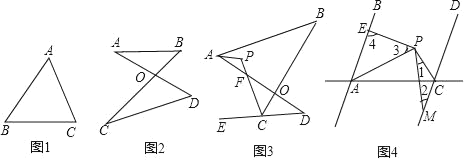
【题目】(1)如图,请证明∠A+∠B+∠C=180°
(2)如图的图形我们把它称为“8字形”,请证明∠A+∠B=∠C+∠D
(3)如图,E在DC的延长线上,AP平分∠BAD,CP平分∠BCE,猜想∠P与∠B、∠D之间的关系,并证明
(4)如图,AB∥CD,PA平分∠BAC,PC平分∠ACD,过点P作PM、PE交CD于M,交AB于E,则①∠1+∠2+∠3+∠4不变;②∠3+∠4﹣∠1﹣∠2不变,选择正确的并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线AB∥射线CD,∠CAB与∠ACD的平分线交于点E,AC=4,点P是射线AB上的一动点,连结PE并延长交射线CD于点Q.给出下列结论:①△ACE是直角三角形;②S四边形APQC=2S△ACE;③设AP=x,CQ=y,则y关于x的函数表达式是y=﹣x+4(0≤x≤4),其中正确的是( )

A. ①②③B. ①②C. ①③D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为D,E.求证:DE=BD+CE;

(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明;若不成立,请说明理由;
(3)如图3,在(2)的条件下,若a=120°,且△ACF为等边三角形,试判断△DEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,若![]() ,将点
,将点![]() 在
在![]() 内部,∠
内部,∠![]() ,∠
,∠![]() ,∠
,∠![]() 满足的数量关系是 ,并说明理由.
满足的数量关系是 ,并说明理由.
(2)在如图1中,将直线![]() 绕点
绕点![]() 逆时针方向旋转一定角度交直线
逆时针方向旋转一定角度交直线![]() 于点
于点![]() ,如图2,利用(1)中的结论(可以直接套用),求∠
,如图2,利用(1)中的结论(可以直接套用),求∠![]() ﹑∠
﹑∠![]() ﹑∠
﹑∠![]() ﹑∠
﹑∠![]() 之间有何数量关系?
之间有何数量关系?

(3)科技活动课上,雨轩同学制作了一个图(3)的“飞旋镖”,经测量发现∠![]() =
=![]() °,∠
°,∠![]() =
=![]() °,则∠
°,则∠![]() 与∠
与∠![]() 的数量关系是 .
的数量关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com