
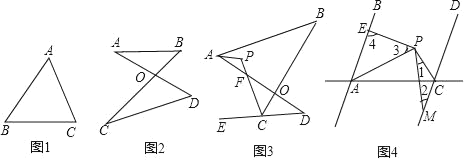
����Ŀ����1����ͼ����֤����A+��B+��C��180��
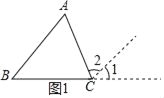
��2����ͼ��ͼ�����ǰ�����Ϊ��8����������֤����A+��B����C+��D
��3����ͼ��E��DC���ӳ����ϣ�APƽ�֡�BAD��CPƽ�֡�BCE�������P���B����D֮��Ĺ�ϵ����֤��
��4����ͼ��AB��CD��PAƽ�֡�BAC��PCƽ�֡�ACD������P��PM��PE��CD��M����AB��E����١�1+��2+��3+��4���䣻�ڡ�3+��4����1����2���䣬ѡ����ȷ�IJ�����֤����
���𰸡���1������������2������������3����P��90��+![]() ����B+��D������4����3+��4����1����2������ȷ�����ɼ�����
����B+��D������4����3+��4����1����2������ȷ�����ɼ�����
��������
��1���ӳ�BC��D������C��CE��BA��������ֱ��ƽ�У�ͬλ����ȿɵá�B����1����ֱ��ƽ�У��ڴ�����ȿɵá�A����2���ٸ���ƽ�ǵĶ�����ʽ�������ɵ�֤��
��2�������������ڽǺͶ�������֤����
��3�����ݣ�2���Ľ��ۡ�B+��BAD����D+��BCD����PAD+��P����D+��PCD��Ȼ���������ɵý⣻
��4����PQ��AB������ƽ�������ʵõ�PQ��CD�����APQ��180������3����4����5����2�����ڡ�APQ+��5+��1��90������180������3����4+��2+��1��90���������õ���3+��4����1����2��90����
��1��֤������ͼ1���ӳ�BC��D������C��CE��BA��
��BA��CE��
���B����1��
��A����2��
�֡ߡ�BCD����BCA+��2+��1��180����
���A+��B+��ACB��180����
��2��֤������ͼ2������AOB�У���A+��B+��AOB��180����

����COD����C+��D+��COD��180����
�ߡ�AOB����COD��
���A+��B����C+��D��
��3����ͼ3��
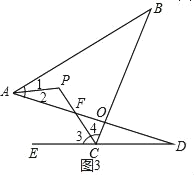
��APƽ�֡�BAD��CPƽ�֡�BCD����ǡ�BCE��
���1����2����3����4��
�ߣ���1+��2��+��B����180����2��3��+��D��
��2+��P����180������3��+��D��
��2��P��180��+��D+��B��
���P��90��+![]() ����B+��D����
����B+��D����
��4���ڡ�3+��4����1����2������ȷ��
�������£�
��PQ��AB����ͼ4��
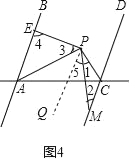
��AB��CD��
��PQ��CD��
��AB��PQ�á�APQ+��3+��4��180��������APQ��180������3����4��
��PQ��CD�á�5����2��
�ߡ�APQ+��5+��1��90����
��180������3����4+��2+��1��90����
���3+��4����1����2��90����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���� ![]() �ı߳�
�ı߳� ![]() ��ijһʱ�̣�����
��ijһʱ�̣����� ![]() ��
�� ![]() �������
������� ![]() ������
������ ![]() ���ٶ���
���ٶ��� ![]() �������˶���ͬʱ������
�������˶���ͬʱ������ ![]() ��
�� ![]() �������
������� ![]() ������
������ ![]() ���ٶ���
���ٶ��� ![]() �������˶����ʣ�
�������˶����ʣ�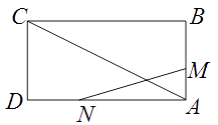
��1����������ʱ�䣬 ![]() ��������ھ���
��������ھ��� ![]() �����
����� ![]() ��
��
��2���Ƿ����ʱ��t��ʹ��A,M,NΪ������������� ![]() ���ƣ������ڣ���t��ֵ���������ڣ���˵�����ɣ�
���ƣ������ڣ���t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����AEƽ�֡�BAF������O�ڵ�E������E��ֱ��ED��AF����AF���ӳ����ڵ�D����AB���ӳ����ڵ�C��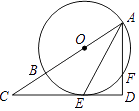
��1����֤��CD�ǡ�O�����ߣ�
��2����tanC= ![]() ����O�İ뾶Ϊ2����DE�ij���
����O�İ뾶Ϊ2����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����Rt��ABC�У���C��90�㣬��A����B����C�ĶԱ߷ֱ�Ϊa��b��c�����ABC�����ΪS���ܳ�Ϊl��
��1�������
����a��b��c |
|
|
3��4��5 | 2 | |
5��12��13 | 4 | |
8��15��17 | 6 |
��2�����![]() ���۲��ϱ����룺
���۲��ϱ����룺 ![]() (�ú���m�Ĵ���ʽ��ʾ)��
(�ú���m�Ĵ���ʽ��ʾ)��
��3��֤����2���еĽ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������BCDE�ĸ��߷ֱ�ƽ����x���y�ᣬ����������ҷֱ��ɵ�A��2��0��ͬʱ�������س�����BCDE�ı��������˶�������װ���ʱ�뷽����1����λ/�������˶��������Ұ�˳ʱ�뷽����2����λ/�������˶��������������˶���ĵ�2017�������ص��������_____��
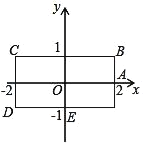
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�п�չһ�����г����λ����·�辭A��B��C��D�ĵأ���ͼ������A��B��C������ͬһֱ���ϣ�D����A�ر�ƫ��30�㷽����C�ر�ƫ��45�㷽��C����A�ر�ƫ��75�㷽����BC=CD=20km������������·��A�ص�D�ص�·�̴�Լ�Ƕ��٣�������������������ο����ݣ�sin15���0.25��cos15���0.97��tan15���0.27�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ABC�ǵȱ������Σ���D���߶�AC�ϵ�һ���㣬E��BC���ӳ����ϣ���BD��DE��
ABC�ǵȱ������Σ���D���߶�AC�ϵ�һ���㣬E��BC���ӳ����ϣ���BD��DE��
��1����ͼ������DΪ�߶�AC���е㣬��֤��AD��CE��
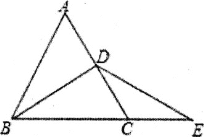
��2����ͼ������DΪ�߶�AC������һ�㣬��֤��AD��CE.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=90�㣬OMƽ�֡�AOB����ֱ�����ǰ�Ķ���P������OM���ƶ�����ֱ�DZ߷ֱ���OA��OB�ཻ�ڵ�C��D����PC��PD�������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ��� ![]() ��ͼ����A��-1��-1���͵�B��3��-9����
��ͼ����A��-1��-1���͵�B��3��-9����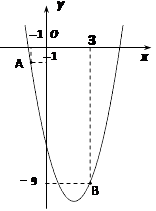
��1����ö��κ����ı���ʽ��
��2��д���������ߵĶԳ��ἰ�������ꣻ
��3����P��m �� m�����Q���ڸú���ͼ���ϣ�����m��0��������������������ߵĶԳ���Գƣ���m��ֵ����Q ��x��ľ��룮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com