
【题目】如图,已知二次函数 ![]() 的图像经过点A(-1,-1)和点B(3,-9).
的图像经过点A(-1,-1)和点B(3,-9).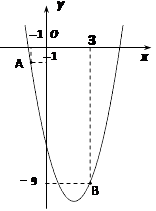
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m , m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的距离.
【答案】
(1)解:将A(﹣1,﹣1)和点B(3,﹣9)代入y=ax2﹣4x+c,
得 ![]() 解得
解得 ![]() ,
,
所以二次函数的表达式为y=x2﹣4x﹣6
(2)解:由y=x2﹣4x﹣6=(x﹣2)2﹣10可知:
对称轴为x=2;顶点坐标为(2,﹣10)
(3)解:将P(m,m)坐标代入y=x2﹣4x﹣6,得m=m2﹣4m﹣6.
解得m1=﹣1,m2=6.
因为m>0,所以m=﹣1不合题意,舍去.所以m=6,
所以P点坐标为(6,6);
因为点P与点Q关于对称轴x=2对称,所以点Q到x轴的距离为46.
【解析】(1)利用待定系数法将点A、点B的坐标代入函数解析式即可求出结果。
(2)利用配方法将函数解析式化成顶点式,即可求出结果。
(3)将点P的坐标代入函数解析式,得出关于m的一元二次方程,解方程求解,根据题意确定m的值,再根据二次函数的对称性求出点Q的坐标。
【考点精析】根据题目的已知条件,利用二次函数的性质的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
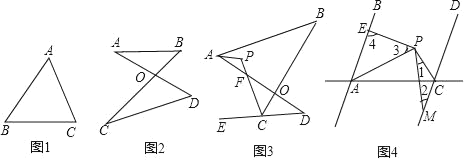
【题目】(1)如图,请证明∠A+∠B+∠C=180°
(2)如图的图形我们把它称为“8字形”,请证明∠A+∠B=∠C+∠D
(3)如图,E在DC的延长线上,AP平分∠BAD,CP平分∠BCE,猜想∠P与∠B、∠D之间的关系,并证明
(4)如图,AB∥CD,PA平分∠BAC,PC平分∠ACD,过点P作PM、PE交CD于M,交AB于E,则①∠1+∠2+∠3+∠4不变;②∠3+∠4﹣∠1﹣∠2不变,选择正确的并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格调查,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式.
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于点C,点D在抛物线上且横坐标为3.
(1)求A、B、C、D的坐标;
(2)求∠BCD的度数;
(3)求tan∠DBC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区为了绿化小区环境,建设和谐家园,准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示,计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价210元,请计算,要完成这块绿化工程,预计花费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,若![]() ,将点
,将点![]() 在
在![]() 内部,∠
内部,∠![]() ,∠
,∠![]() ,∠
,∠![]() 满足的数量关系是 ,并说明理由.
满足的数量关系是 ,并说明理由.
(2)在如图1中,将直线![]() 绕点
绕点![]() 逆时针方向旋转一定角度交直线
逆时针方向旋转一定角度交直线![]() 于点
于点![]() ,如图2,利用(1)中的结论(可以直接套用),求∠
,如图2,利用(1)中的结论(可以直接套用),求∠![]() ﹑∠
﹑∠![]() ﹑∠
﹑∠![]() ﹑∠
﹑∠![]() 之间有何数量关系?
之间有何数量关系?

(3)科技活动课上,雨轩同学制作了一个图(3)的“飞旋镖”,经测量发现∠![]() =
=![]() °,∠
°,∠![]() =
=![]() °,则∠
°,则∠![]() 与∠
与∠![]() 的数量关系是 .
的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在反比例函数 ![]() 的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为C,且△AOC的面积为2,
的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为C,且△AOC的面积为2,
(1)求该反比例函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com