
【题目】如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于点C,点D在抛物线上且横坐标为3.
(1)求A、B、C、D的坐标;
(2)求∠BCD的度数;
(3)求tan∠DBC的值.
【答案】
(1)解:令y=0,则﹣x2+3x+4=0,
即(x+1)(x﹣4)=0.
解得:x1=﹣1,x2=4.
所以A(﹣1,0),B(4,0),
令x=0,得y=4,所以C(0,4),
当x=3时,y=﹣32+3×3+4=4,
所以D(3,4)。
(2)解:∵OC=OB=4,
∴∠ABC=45°,
∵C、D的纵坐标相同,
∴CD∥AB.
又∵OC=OB,
∴∠BCD=∠OBC=45°
(3)解:过点D作DE⊥BC于点E, 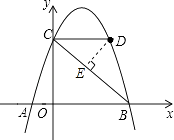
在Rt△OBC中,得BC=4 ![]() ,
,
在Rt△CDE中,∵CD=3,
∴CE=ED= ![]()
![]() ,
,
∴BE=BC﹣CE= ![]()
![]() ,
,
∴tan∠DBC= ![]() =
= ![]() .
.
【解析】(1)将y=0和x=0,x=3分别代入函数解析式,求出对应的自变量的值和对应的函数值,即可求出A、B、C、D的坐标。
(2)根据点B的横坐标和点C的纵坐标相等,即可证出△OBC是等腰直角三角形,得出∠ABC=45°,再观察点C、点D的纵坐标相等得出CD∥AB,根据平行线的性质即可求出结果。
(3)添加辅助线将∠DBC转化到直角三角形中,因此过点D作DE⊥BC于点E,先根据点C和点D的坐标求出CD的长,在Rt△OBC中和在Rt△CDE中分别求出BC、DE的长,就可以求出BE的长,从而求得结果。
【考点精析】掌握抛物线与坐标轴的交点和勾股定理的概念是解答本题的根本,需要知道一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】某市开展一项自行车旅游活动,线路需经A,B,C,D四地,如图,其中A,B,C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两个全等的直角三角形△ABD、△ACE拼在一起(图(1)).令△ABD不动,
(1)若将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC(图(2)),证明:MB=MC.
(2)若将图(1)中的CE向上平移,∠CAE不变,连接DE,M是DE的中点,连接MB、MC(图(3)),判断MB、MC的数量关系,并说明理由.
(3)在(2)中,若∠CAE的大小改变(图(4)),其他条件不变,则(2)中的MB、MC的数量关系还成立吗?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数 ![]() 的图像经过点A(-1,-1)和点B(3,-9).
的图像经过点A(-1,-1)和点B(3,-9).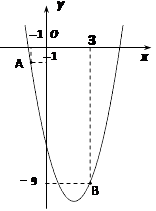
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m , m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于任何数a,符号[a]表示不大于a的最大整数.
例如:[5.7]=5,[5]=5,[﹣1.5]=﹣2.
(1)[﹣![]() ]= ;
]= ;
(2)如果[a]=3,那么a的取值范围是 ;
(3)如果[![]() ]=﹣3,求满足条件的所有整数x.
]=﹣3,求满足条件的所有整数x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着市民环保意识的增强,节庆期间烟花爆竹销售量逐年下降.某市2012年销售烟花爆竹20万箱,到2014年烟花爆竹销售量为9.8万箱.求该市2012年到2014年烟花爆竹年销售量的平均下降率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).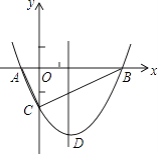
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com