
【题目】如图,抛物线y= ![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).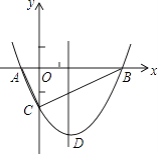
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
【答案】
(1)解:∵点A(﹣1,0)在抛物线y= ![]() x2+bx﹣2上,
x2+bx﹣2上,
∴ ![]() ×(﹣1 )2+b×(﹣1)﹣2=0,
×(﹣1 )2+b×(﹣1)﹣2=0,
解得:b=﹣ ![]() ,
,
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣2.
x﹣2.
y= ![]() (x﹣
(x﹣ ![]() )2﹣
)2﹣ ![]() ,
,
∴顶点D的坐标为:( ![]() ,﹣
,﹣ ![]() )
)
(2)解:当x=0时y=﹣2,∴C(0,﹣2),OC=2.
当y=0时, ![]() x2﹣
x2﹣ ![]() x﹣2=0,
x﹣2=0,
解得:x1=﹣1,x2=4,
∴B (4,0),
∴OA=1,OB=4,AB=5.
∵AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,
∴AC2+BC2=AB2.
∴△ABC是直角三角形.
(3)解:如图所示:连接AM,

点A关于对称轴的对称点B,BC交对称轴于点M,根据轴对称性及两点之间线段最短可知,
MC+MA的值最小,即△ACM周长最小,
设直线BC解析式为:y=kx+d,则 ![]() ,
,
解得: 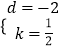 ,
,
故直线BC的解析式为:y= ![]() x﹣2,
x﹣2,
当x= ![]() 时,y=﹣
时,y=﹣ ![]() ,
,
∴M( ![]() ,﹣
,﹣ ![]() ),
),
△ACM最小周长是:AC+AM+MC=AC+BC= ![]() +2
+2 ![]() =3
=3 ![]() .
.
【解析】(1)将点A的坐标代入抛物线的解析式即可求出b的值;再将二次函数配方成顶点式,即可写出顶点坐标。
(2)先求出抛物线与x轴、y轴的交点坐标,即求出当x=0时y的值和y=0时x的值,再利用勾股定理求出AB2,AC2,BC2,再比较AC2+BC2与AB2的大小即可判断。
(3)抓住已知条件点M是抛物线对称轴上的一个动点且当△ACM周长最小,可知点A和点B关于抛物线的对称轴对称,因此连接BC交对称轴于点M,连接AM,先求出直线BC的函数解析式,再根据抛物线的顶点坐标即可求出点,M的坐标,然后利用勾股定理求出BC、AC的长,△ACM的最小周长=BC+AC,即可求出结果。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对抛物线与坐标轴的交点的理解,了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于点C,点D在抛物线上且横坐标为3.
(1)求A、B、C、D的坐标;
(2)求∠BCD的度数;
(3)求tan∠DBC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家快递公司揽件员(揽收快件的员工)的日工资方案如下:
甲公司为“基本工资+揽件提成”,其中基本工资为70元/日,每揽收一件提成2元;
乙公司无基本工资,仅以揽件提成计算工资.若当日揽件数不超过40,每件提成4元;若当日搅件数超过40,超过部分每件多提成2元.
如图是今年四月份甲公司揽件员人均揽件数和乙公司搅件员人均揽件数的条形统计图:
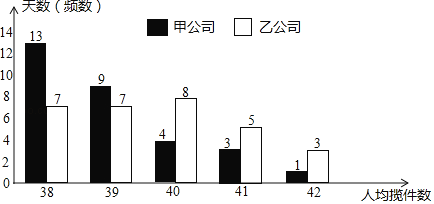
(1)现从今年四月份的30天中随机抽取1天,求这一天甲公司揽件员人均揽件数超过40(不含40)的概率;
(2)根据以上信息,以今年四月份的数据为依据,并将各公司揽件员的人均揽件数视为该公司各揽件员的
揽件数,解决以下问题:
①估计甲公司各揽件员的日平均件数;
②小明拟到甲、乙两家公司中的一家应聘揽件员,如果仅从工资收入的角度考虑,请利用所学的统计知识帮他选择,井说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于雾霾天气持续笼罩某地区,口罩市场出现热卖.某商店用8000元购进甲、乙两种口罩,销售完后共获利2800元,其进价和售价如下表:
甲种口罩 | 乙种口罩 | |
进价(元/袋) | 20 | 25 |
售价(元/袋) | 26 | 35 |
(1)求该商店购进甲、乙两种口罩各多少袋?
(2)该商店第二次仍以原价购进甲、乙两种口罩,购进乙种口罩袋数不变,而购进甲种口罩袋数是第一次的2倍,甲种口罩按原售价出售,而乙种口罩让利销售.若两种口罩销售完毕,要使第二次销售活动获利不少于3680元,则乙种口罩最低售价为每袋多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在反比例函数 ![]() 的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为C,且△AOC的面积为2,
的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为C,且△AOC的面积为2,
(1)求该反比例函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
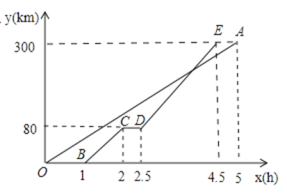
【题目】甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发驶向乙地。如图,线段OA表示货车离甲地的距离![]() (km)与时间
(km)与时间![]() (h)之间的函数关系,折线BCDE变式轿车离甲地的距离
(h)之间的函数关系,折线BCDE变式轿车离甲地的距离![]() (km)与时间
(km)与时间![]() (h)之间的函数关系。根据图像,解答下列问题:
(h)之间的函数关系。根据图像,解答下列问题:
(1)线段CD表示轿车在途中停留了 h.
(2)求线段DE对应的函数关系式(2.5≤x≤4.5).
(3)求轿车从甲地出发后经过多长时间追上货车.
查看答案和解析>>
科目:初中数学 来源: 题型:
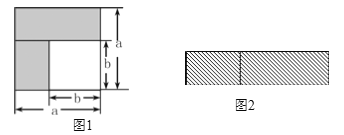
【题目】乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2两图的阴影部分面积,可以得到乘法公式 (用式子表达);
(4)运用你所得到的公式,计算下列各题:
①(2m+n-p)(2m-n+p);②10.3×9.7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用火柴棒摆出一列正方形图案,第①个图案用了 4 根,第②个图案用了 12 根,第③个图案用了 24 根,按照这种方式摆下去,摆出第⑥个图案用火柴棒的根数是( )

A. 84 B. 81 C. 78 D. 76
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com