
【题目】如图,点A、B在反比例函数 ![]() 的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为C,且△AOC的面积为2,
的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为C,且△AOC的面积为2,
(1)求该反比例函数的解析式;
(2)求△AOB的面积.
【答案】
(1)∵S△AOC=2,
∴k=2S△AOC=4;
∴y= ![]() ;
;
(2)解:连接AB,过点B作BE⊥x轴, 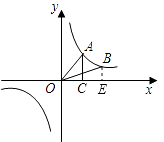
S△AOC=S△BOE=2,
∴A(a, ![]() ),B(2a,
),B(2a, ![]() );
);
S梯形ACEB= ![]() (
( ![]() +
+ ![]() )×(2a﹣a)=3,
)×(2a﹣a)=3,
∴S△AOB=S△AOC+S梯形ACEB﹣S△BOE=3.
【解析】(1)根据反比例函数系数k的几何意义,可知S△AOC=![]() |k|,由图像可知k>0,即可求出反比例函数的解析式。
|k|,由图像可知k>0,即可求出反比例函数的解析式。
(2)连接AB,过点B作BE⊥x轴, 观察图像可知S△AOB=S△AOC+S梯形ACEB﹣S△BOE。根据反比例函数系数k的几何意义,可知S△AOC=S△BOE=2,只需求出梯形ACEB的面积,根据A、B两点的坐标及梯形的面积公式易求出它的面积,从而可求得结果。
【考点精析】解答此题的关键在于理解反比例函数的图象的相关知识,掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点,以及对比例系数k的几何意义的理解,了解几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,已知二次函数 ![]() 的图像经过点A(-1,-1)和点B(3,-9).
的图像经过点A(-1,-1)和点B(3,-9).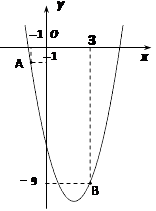
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m , m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D。
(1)求证:BC是⊙O切线;
(2)若BD=5, DC=3,求AC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在山顶上有一座电视塔,在塔顶B处,测得地面上一点A的俯角α=60°,在塔底C处测得的俯角β=45°,已知BC=60m,求山高CD(精确到1m, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
如图,∠1+∠2=1800,∠3=∠4.
求证:EF∥GH.

证明:∵∠1+∠2=1800(已知),
∠AEG =∠1(对顶角相等)
∴ ,
∴AB∥CD( ),
∴∠AEG=∠ ( ),
∵∠3=∠4(已知),
∴∠3+∠AEG=∠4+∠ ,(等式性质)
∴ ,
∴EF∥GH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).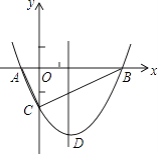
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1 , 再以正方形的对角线OA2作正方形OA1A2B1 , …,依此规律,则点A8的坐标是( )
A.(﹣8,0)
B.(0,8)
C.(0,8 ![]() )
)
D.(0,16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:(不写作法,但必须保留作图痕迹)
如图:某地有两所大学和两条相交叉的公路,(点M,N表示大学,AO,BO表示公路).现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库P应该建在什么位置吗?在所给的图形中画出你的设计方案.
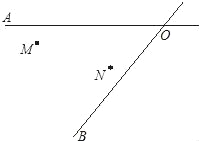
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,沿CA方向运动,速度是2cm/s,动点Q从点B出发,沿BC方向运动,速度是1cm/s.
(1)几秒后P、Q两点相距25cm?
(2)几秒后△PCQ与△ABC相似?
(3)设△CPQ的面积为S1 , △ABC的面积为S2 , 在运动过程中是否存在某一时刻t,使得S1:S2=2:5?若存在,求出t的值;若不存在,则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com