
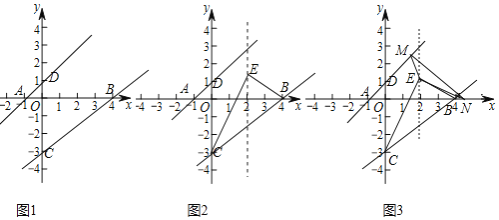
【题目】如图1,点A、B、C在坐标轴上,且A、B、C的坐标分别为![]() 、
、![]() 、
、![]() 过点A的直线AD与y轴正半轴交于点D,
过点A的直线AD与y轴正半轴交于点D,![]()
![]() 求直线AD和BC的解析式;
求直线AD和BC的解析式;
![]() 如图2,点E在直线
如图2,点E在直线![]() 上且在直线BC上方,当
上且在直线BC上方,当![]() 的面积为6时,求E点坐标;
的面积为6时,求E点坐标;
![]() 在
在![]() 的条件下,如图3,动点M在直线AD上,动点N在x轴上,连接ME、NE、MN,当
的条件下,如图3,动点M在直线AD上,动点N在x轴上,连接ME、NE、MN,当![]() 周长最小时,求
周长最小时,求![]() 周长的最小值.
周长的最小值.
【答案】![]() ,
,![]() ;
;![]() 点E的坐标为
点E的坐标为![]() ;
;![]() 周长的最小值
周长的最小值![]() .
.
【解析】
(1)∠DAB=45°,OA=DO=1,即点D的坐标为(0,1),将点A、D的坐标代入一次函数表达式,即可求解;
![]() 由
由![]() ,即可求解;
,即可求解;
(3)作点E关于直线AD对称点![]() ;找到点E关于x轴的对称点
;找到点E关于x轴的对称点![]() ,连接
,连接![]() 交AD于M点、交x轴于点N,则△MNE周长最小,即可求解.
交AD于M点、交x轴于点N,则△MNE周长最小,即可求解.
![]() ,
,
![]() ,即点D的坐标为
,即点D的坐标为![]() ,
,
将点A、D的坐标代入一次函数表达式:![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
则直线AD的表达式为:![]() ,
,
同理可得直线BC的表达式为:![]() ;
;
![]() 设直线
设直线![]() 与BC交于点F,点E坐标为
与BC交于点F,点E坐标为![]() ,则点F坐标为
,则点F坐标为![]() ,
,
则![]() ,解得:
,解得:![]() ,
,
即点E的坐标为![]() ;
;
![]() 过点E点作
过点E点作![]() ,点E和
,点E和![]() 关于直线AD对称,
关于直线AD对称,
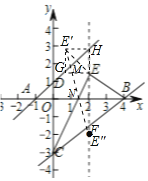
设直线![]() 与直线AD交于点
与直线AD交于点![]() ,连接
,连接![]() ,
,
找到点E关于x轴的对称点![]() ,
,
连接![]() 交AD于M点、交x轴于点N,此时,
交AD于M点、交x轴于点N,此时,![]() 周长最小,
周长最小,
![]() ,
,
![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
则:![]() 周长的最小值
周长的最小值![]() .
.
故答案为:(1)y=x+1,y=![]() x-3;(2)点E的坐标为
x-3;(2)点E的坐标为![]() ;(3)△MNE周长的最小值
;(3)△MNE周长的最小值![]() .
.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,已知矩形 ![]() 的边长
的边长 ![]() .某一时刻,动点
.某一时刻,动点 ![]() 从
从 ![]() 点出发沿
点出发沿 ![]() 方向以
方向以 ![]() 的速度向
的速度向 ![]() 点匀速运动;同时,动点
点匀速运动;同时,动点 ![]() 从
从 ![]() 点出发沿
点出发沿 ![]() 方向以
方向以 ![]() 的速度向
的速度向 ![]() 点匀速运动,问:
点匀速运动,问: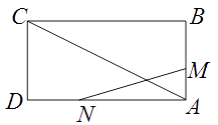
(1)经过多少时间, ![]() 的面积等于矩形
的面积等于矩形 ![]() 面积的
面积的 ![]() ?
?
(2)是否存在时刻t,使以A,M,N为顶点的三角形与 ![]() 相似?若存在,求t的值;若不存在,请说明理由.
相似?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明乘坐家门口的公交车到和平公园游玩,他先乘坐公交车0.8小时后达到书城,逗留一段时间后继续坐公交车到和平公园,小明出发一段时间后,小明的妈妈不放心,于是驾车沿相同的路线前往和平公园,如图是他们离家的路程![]() 与离家时间
与离家时间![]() 的关系图,请根据图回答下列问题:
的关系图,请根据图回答下列问题:
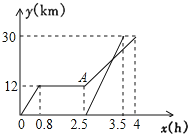
(1)小明家到和平公园的路程为 ![]() ,他在书城逗留的时间为
,他在书城逗留的时间为 ![]() ;
;
(2)图中![]() 点表示的意义是 ;
点表示的意义是 ;
(3)求小明的妈妈驾车的平均速度(平均速度=![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠A=90°,BC=10cm,点P、点Q同时从点B出发,点P以2cm/s的速度沿B→A→C运动,终点为C,点Q以1cm/s的速度沿B→C运动,当点P到达终点时两个点同时停止运动,设点P,Q出发t秒时,△BPQ的面积为ycm2 , 已知y与t的函数关系的图象如图2(曲线OM和MN均为抛物线的一部分),给出以下结论:①AC=6cm;②曲线MN的解析式为y=﹣ ![]() t2+
t2+ ![]() t(4≤t≤7);③线段PQ的长度的最大值为
t(4≤t≤7);③线段PQ的长度的最大值为 ![]() ;④若△PQC与△ABC相似,则t=
;④若△PQC与△ABC相似,则t= ![]() 秒.其中正确的是( )
秒.其中正确的是( )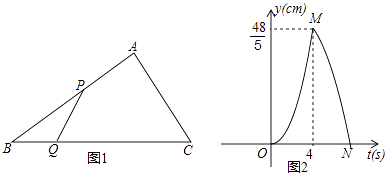
A.①②④
B.②③④
C.①③④
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.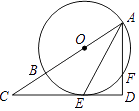
(1)求证:CD是⊙O的切线;
(2)若tanC= ![]() ,⊙O的半径为2,求DE的长.
,⊙O的半径为2,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,设△ABC的面积为S,周长为l.
(1)填表:
三边a、b、c |
|
|
3、4、5 | 2 | |
5、12、13 | 4 | |
8、15、17 | 6 |
(2)如果![]() ,观察上表猜想:
,观察上表猜想: ![]() (用含有m的代数式表示).
(用含有m的代数式表示).
(3)证明(2)中的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OM平分∠AOB,将直角三角板的顶点P在射线OM上移动,两直角边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com