
����Ŀ����ͼ1����Rt��ABC�У���A=90�㣬BC=10cm����P����Qͬʱ�ӵ�B��������P��2cm/s���ٶ���B��A��C�˶����յ�ΪC����Q��1cm/s���ٶ���B��C�˶�������P�����յ�ʱ������ͬʱֹͣ�˶������P��Q����t��ʱ����BPQ�����Ϊycm2 �� ��֪y��t�ĺ�����ϵ��ͼ����ͼ2������OM��MN��Ϊ�����ߵ�һ���֣����������½��ۣ���AC=6cm��������MN�Ľ���ʽΪy=�� ![]() t2+
t2+ ![]() t��4��t��7�������߶�PQ�ij��ȵ����ֵΪ
t��4��t��7�������߶�PQ�ij��ȵ����ֵΪ ![]() ��������PQC���ABC���ƣ���t=
��������PQC���ABC���ƣ���t= ![]() �룮������ȷ���ǣ� ��
�룮������ȷ���ǣ� ��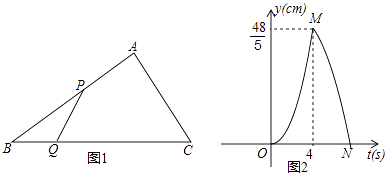
A.�٢ڢ�
B.�ڢۢ�
C.�٢ۢ�
D.�٢ڢ�
���𰸡�A
����������ͼ2�ɵõ�t=4ʱ��y= 48 5 ��
��AB=2��4=8cm��
�ߡ�A=90�㣬BC=10cm��
��AC=6cm��
�ʢ���ȷ��
�ڵ�P��AC��ʱ����ͼ3����P��PD��BC��D��
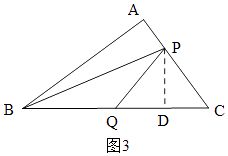
��ʱ�� ![]() =7��
=7��
��4��t��7��
������ã�AB+AP=2t��BQ=t��
��PC=14��2t��
sin��C= ![]() ��
��
�� ![]() =
= ![]() ��
��
��PD= ![]() ��
��
��y=S��BPQ= ![]() BQPD=
BQPD= ![]() t
t ![]() =��
=�� ![]() ��
��
�ʢ���ȷ��
�۵�P��A�غ�ʱ��PQ�����ͼ4����ʱt=4��
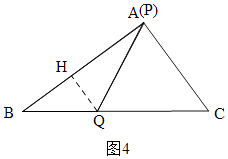
��BQ=4��
��Q��GH��AB��H��
sin�� ![]() ��
��
�� ![]() ��
��
��QH= ![]() ��
��
ͬ����BH= ![]() ��
��
��AH=8�� ![]() =
= ![]() ��
��
��PQ= ![]() =
= ![]() =
= ![]() ��
��
���߶�PQ�ij��ȵ����ֵΪ ![]() ��
��
�ʢ۲���ȷ��
������PQC���ABC���ƣ���Pֻ�����߶�AC�ϣ�
�����������
PC=14��2t��QC=10��t��
i������CPQ�ס�CBA����ͼ5���� ![]() ��
��
�� ![]() ��
��
���t=��8�������⣮
ii������PQC�ס�BACʱ����ͼ5��
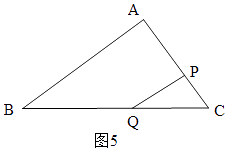
�� ![]() ��
��
�� ![]() ��
��
t= ![]() ��
��
������PQC���ABC���ƣ���t= ![]() �룬
�룬
�ʢ���ȷ��
������ȷ���У��٢ڢ�.
���Դ��ǣ�A��


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������A1��1��0����x��Ĵ��ߣ���ֱ��y��2x�ڵ�B1����A2���O����ֱ��A1B1�Գƣ�����A2��2��0����x��Ĵ��ߣ���ֱ��y��2x�ڵ�B2����A3���O����ֱ��A2B2�Գƣ�����A3��4��0����x��Ĵ��ߣ���ֱ��y��2x�ڵ�B3���������˹�������ȥ�����Bn������Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���
��1��̽����֪����ͼ1����֪��ABC���ABD�������ȣ����ж�AB��CD��λ�ù�ϵ����˵�����ɣ�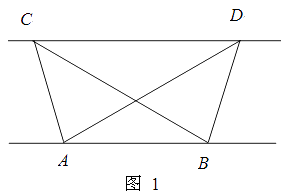
��2������Ӧ�ã��� ��ͼ2����M��N�ڷ��������� ![]() ��k��0����ͼ���ϣ�����M��ME��y�ᣬ����N��NF��x�ᣬ����ֱ�ΪE��F����֤����MN��EF��
��k��0����ͼ���ϣ�����M��ME��y�ᣬ����N��NF��x�ᣬ����ֱ�ΪE��F����֤����MN��EF�� 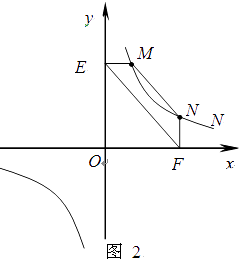
�� �����е������������䣬ֻ�ı��M��N��λ����ͼ3��ʾ�����ж� MN��EF�Ƿ�ƽ�У���˵������.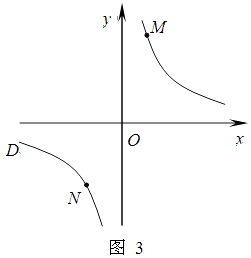
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����������y= ![]() ��x��0����ͼ����A��1��2���͵�B��m��n����m��1��������B��y��Ĵ��ߣ�����ΪC��
��x��0����ͼ����A��1��2���͵�B��m��n����m��1��������B��y��Ĵ��ߣ�����ΪC��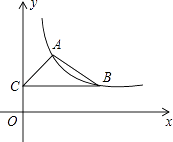
��1����÷�������������ʽ��
��2������ABC���Ϊ2ʱ�����B�����꣮
��3��PΪ�߶�AB��һ���㣨P����A��B�غϣ����ڣ�2��������£�ֱ��y=ax��1���߶�AB���ڵ�P��ֱ��д��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
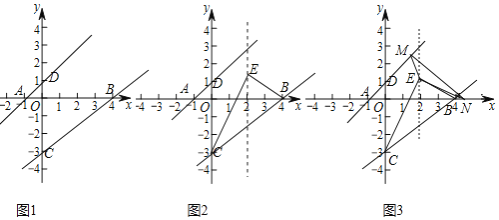
����Ŀ����ͼ1����A��B��C���������ϣ���A��B��C������ֱ�Ϊ![]() ��
��![]() ��
��![]() ����A��ֱ��AD��y�������ύ�ڵ�D��
����A��ֱ��AD��y�������ύ�ڵ�D��![]()
![]() ��ֱ��AD��BC�Ľ���ʽ��
��ֱ��AD��BC�Ľ���ʽ��
![]() ��ͼ2����E��ֱ��
��ͼ2����E��ֱ��![]() ������ֱ��BC�Ϸ�����
������ֱ��BC�Ϸ�����![]() �����Ϊ6ʱ����E�����ꣻ
�����Ϊ6ʱ����E�����ꣻ
![]() ��
��![]() �������£���ͼ3������M��ֱ��AD�ϣ�����N��x���ϣ�����ME��NE��MN����
�������£���ͼ3������M��ֱ��AD�ϣ�����N��x���ϣ�����ME��NE��MN����![]() �ܳ���Сʱ����
�ܳ���Сʱ����![]() �ܳ�����Сֵ��
�ܳ�����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��3��5����ѧ���գ�ijУ��֯���ԡ�����ͬ־ѧϰ��Ϊ�����С���������������ֽ��ֻ��60��70��80��90��100���֣��ִ��������ȡ������Ʒ������������ɼ������������Ƴ�����������������ͳ��ͼ������������Ϣ������������⣺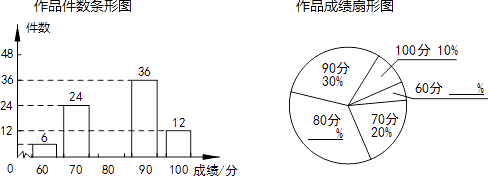
��1���γ�ȡ�˶��ٷ���Ʒ������ȫ����ͳ��ͼ��
��2����֪��У�յ�������Ʒ��1200�ݣ�����Ƹ�Уѧ�������ɼ��ﵽ90�����ϣ���90�֣�����Ʒ�ж��ٷݣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+ ![]() x+1��a��0����x�ύ��A��B���㣬���е�B����Ϊ��2��0����
x+1��a��0����x�ύ��A��B���㣬���е�B����Ϊ��2��0����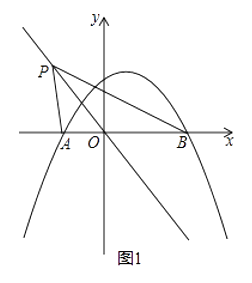
��1���������ߵĽ���ʽ�͵�A�����ꣻ
��2����ͼ1����P��ֱ��y=��x�ϵĶ��㣬��ֱ��OPƽ�֡�APBʱ�����P�����ꣻ
��3����ͼ2���ڣ�2���������£���C��ֱ��BP�Ϸ����������ϵ�һ�����㣬����C��y���ƽ���ߣ���ֱ��BP�ڵ�D����E��ֱ��BP�ϣ�����CE����CDΪ���ĵ�����CDE������Ƿ�������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�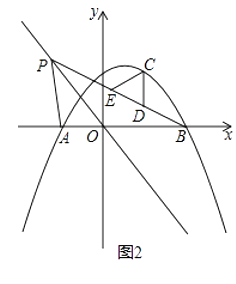
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOP����BOP��15�㣬PC��OA��PD��OA����PC��4����PD�ij�Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1������ABC�У���BAC��90����AB��AC��ֱ��m������A��BD��ֱ��m��CE��ֱ��m������ֱ�ΪD��E����֤��DE��BD+CE��

��2����ͼ2������1���е�������Ϊ������ABC�У�AB��AC��D��A��E���㶼��ֱ��m�ϣ������С�BDA����AEC����BAC��a������aΪ������ǻ�۽ǣ����ʽ���DE��BD+CE�Ƿ���������������������֤����������������˵�����ɣ�
��3����ͼ3���ڣ�2���������£���a��120��������ACFΪ�ȱ������Σ����ж���DEF����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com