
分析 对于$\left\{\begin{array}{l}{x+2y+3z=4①}\\{y+z=1②}\\{3x+2z=3③}\end{array}\right.$,先由②③变形,用z表示x和y,再把它们代入①得到关于z的一元一次方程,解方程求出z,然后分别计算出x和y的值,从而得到方程组的解.
解答 解:$\left\{\begin{array}{l}{x+2y+3z=4①}\\{y+z=1②}\\{3x+2z=3③}\end{array}\right.$,
由②得y=1-z④,
由③得x=$\frac{3-2z}{3}$⑤,
把④⑤代入①得$\frac{3-2z}{3}$+2(1-z)+3z=4,
解得z=3,
则y=1-3=-2,x=$\frac{3-2×3}{3}$=-1,
所以方程组的解为$\left\{\begin{array}{l}{x=-1}\\{y=-2}\\{z=3}\end{array}\right.$.
点评 本题考查了解三元一次方程组:利用代入法或加减法,把解三元一次方程组的问题转化为解二元一次方程组得问题.


科目:初中数学 来源: 题型:解答题
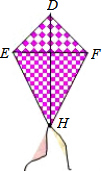 为参加学校举办的风筝设计比赛,小明用四根竹棒扎成如图所示的风筝框架,其中∠EDH=∠FDH,ED=FD.将上述条件标注在图中,小明不用测量就能知道EH=FH吗?为什么?
为参加学校举办的风筝设计比赛,小明用四根竹棒扎成如图所示的风筝框架,其中∠EDH=∠FDH,ED=FD.将上述条件标注在图中,小明不用测量就能知道EH=FH吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com