
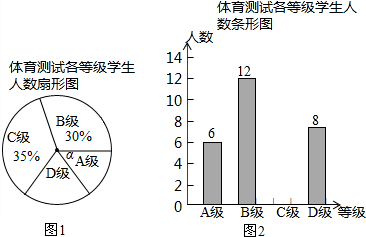
���� ��1����B��������������ռ�İٷֱ������������
��2����360�����A����ռ�İٷֱ�����Ϧ��Ķ�����������������ȥA��B��D�������������C�����������Ӷ���ȫͳ��ͼ��
��3���þ��꼶���е�ѧ�������Բ������������ռ�İٷֱȣ�����������������
��4���������⻭����״ͼ���ٸ��ݸ��ʹ�ʽ���м��㼴�ɣ�
��� �⣺��1�����γ������Ե�ѧ�������ǣ�$\frac{12}{30%}$=40���ˣ���
�ʴ�Ϊ��40��
��2����������ã�360���$\frac{6}{40}$=54�㣻C���������ǣ�40-6-12-8=14���ˣ���
�ʴ�Ϊ��54�㣻
��ͼ��ʾ��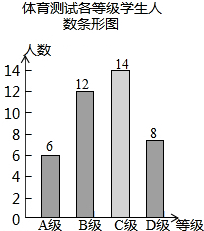
��3����������ã�7200��$\frac{8}{40}$=1440���ˣ���
�ʴ�Ϊ��1440�ˣ�
��4���������⻭����ͼ���£�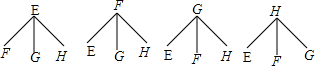
����12�������ѡ��С������6�֣���P��ѡ��С����=$\frac{6}{12}$=$\frac{1}{2}$��
���� ���⿼��������ͳ��ͼ������ͳ��ͼ���ۺ�Ӧ�ã��õ���֪ʶ�����������������塢Ƶ����Ƶ�ʡ�����֮��Ĺ�ϵ�ȣ�����ͳ��ͼ���Ӳ�ͬ��ͳ��ͼ�еõ���Ҫ����Ϣ�ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��$\frac{1}{2}$ | B�� | x��$\frac{1}{2}$ | C�� | x��$\frac{1}{2}$ | D�� | x��$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a3+a3=a6 | B�� | 2��a+1��=2a+1 | C�� | ��-ab��2=a2b2 | D�� | a6��a3=a2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
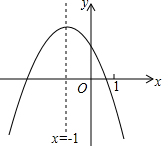 ���κ���y=ax2+bx+c��a��0����ͼ����ͼ�����������ĸ����ۣ�
���κ���y=ax2+bx+c��a��0����ͼ����ͼ�����������ĸ����ۣ�| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com