
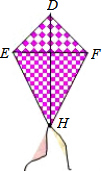
 为参加学校举办的风筝设计比赛,小明用四根竹棒扎成如图所示的风筝框架,其中∠EDH=∠FDH,ED=FD.将上述条件标注在图中,小明不用测量就能知道EH=FH吗?为什么?
为参加学校举办的风筝设计比赛,小明用四根竹棒扎成如图所示的风筝框架,其中∠EDH=∠FDH,ED=FD.将上述条件标注在图中,小明不用测量就能知道EH=FH吗?为什么? 科目:初中数学 来源: 题型:选择题
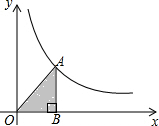 如图,在直角坐标系中,点A是双曲线y=$\frac{3}{x}$(x>0)上的一个动点,过点A作AB⊥x轴于点B.当点A的横坐标逐渐增大时,△OAB的面积将会( )
如图,在直角坐标系中,点A是双曲线y=$\frac{3}{x}$(x>0)上的一个动点,过点A作AB⊥x轴于点B.当点A的横坐标逐渐增大时,△OAB的面积将会( )| A. | 逐渐增大 | B. | 不变 | C. | 先增大后减小 | D. | 逐渐减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com