
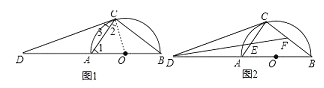
【题目】如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;
①求tan∠CFE的值;
②若AC=3,BC=4,求CE的长.

【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OC,根据切线的性质、直径所对的圆周角是直角及等角的余角相等即可证明结论.
(2)①由∠CEF=∠ECD+∠CDE,∠CFE=∠B+∠FDB,∠CDE=∠FDB,∠ECD=∠B,即可得∠CEF=∠CF,再由∠ECF=90°,可得∠CEF=∠CFE=45°,即可得结论.
②由勾股定理可求得AB=5,根据已知易证△DCA∽△DBC,得![]() ,设DC=3k,DB=4k,由CD2=DADB,得9k2=(4k﹣5)4k,由此求出DC,DB,再由△DCE∽△DBF,得
,设DC=3k,DB=4k,由CD2=DADB,得9k2=(4k﹣5)4k,由此求出DC,DB,再由△DCE∽△DBF,得![]() ,设EC=CF=x,列出方程即可解决问题.
,设EC=CF=x,列出方程即可解决问题.
试题解析:(1)证明:如图1中,连接OC.
∵OA=OC,
∴∠1=∠2,
∵CD是⊙O切线,
∴OC⊥CD,
∴∠DCO=90°,
∴∠3+∠2=90°,
∵AB是直径,
∴∠1+∠B=90°,
∴∠3=∠B.
(2)解:①∵∠CEF=∠ECD+∠CDE,∠CFE=∠B+∠FDB,
∵∠CDE=∠FDB,∠ECD=∠B,
∴∠CEF=∠CFE,∵∠ECF=90°,
∴∠CEF=∠CFE=45°,
∴tan∠CFE=tan45°=1.
②在RT△ABC中,∵AC=3,BC=4,
由勾股定理得AB=5,
∵∠CDA=∠BDC,∠DCA=∠B,
∴△DCA∽△DBC,
∴![]() ,设DC=3k,DB=4k,
,设DC=3k,DB=4k,
∵CD2=DADB,
∴9k2=(4k﹣5)4k,
∴k=![]() ,
,
∴CD=![]() ,DB=
,DB=![]() ,
,
∵∠CDE=∠BDF,∠DCE=∠B,
∴△DCE∽△DBF,
∴![]() ,设EC=CF=x,
,设EC=CF=x,
∴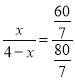 ,
,
∴x=![]() .
.
∴CE=![]() .
.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查,调查的项目有:公共汽车、小车、摩托车、自行车、其它(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
交通方式 | 频数(人数) | 频率 |
公共汽车 | m | 0.25 |
小车 | 24 | 0.20 |
摩托车 | 36 | n |
自行车 | 18 | 0.15 |
其它 | 12 | 0.10 |
请根据图表信息解答下列问题:
(1)本次共抽样调查个学生;
(2)填空:频数分布表中的m= , n=;
(3)在扇形统计图中,请计算出“摩托车”所在的扇形的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】9名学生的体重分别是41、48、50、53、49、53、53、51、67(单位:kg),这组数据的众数是( )
A. 41 B. 48
C. 53 D. 67
查看答案和解析>>
科目:初中数学 来源: 题型:
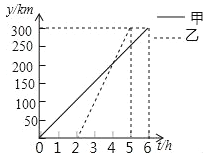
【题目】甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
①甲车的速度为50km/h ②乙车用了3h到达B城
③甲车出发4h时,乙车追上甲车 ④乙车出发后经过1h或3h两车相距50km.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在100名学生中抽查了40名学生的数学成绩,按成绩共分成6组,第1~4组的人数分别为10,5,7,6,第5组的百分比为10%,则第6组的百分比为( )
A. 25% B. 30% C. 15% D. 20%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com