
【题目】某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查,调查的项目有:公共汽车、小车、摩托车、自行车、其它(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
交通方式 | 频数(人数) | 频率 |
公共汽车 | m | 0.25 |
小车 | 24 | 0.20 |
摩托车 | 36 | n |
自行车 | 18 | 0.15 |
其它 | 12 | 0.10 |
请根据图表信息解答下列问题:
(1)本次共抽样调查个学生;
(2)填空:频数分布表中的m= , n=;
(3)在扇形统计图中,请计算出“摩托车”所在的扇形的圆心角的度数.
科目:初中数学 来源: 题型:
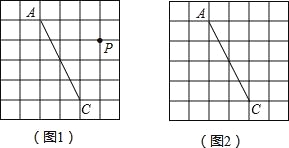
【题目】图1、图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.
(1)如图1,点P在小正方形的顶点上,在图1中作出点P关于直线AC的对称点Q,连接AQ、QC、CP、PA,并直接写出四边形AQCP的周长;
(2)在图2中画出一个以线段AC为对角线、面积为6的矩形ABCD,且点B和点D均在小正方形的顶点上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,现有一张三角形ABC纸片,沿BC边上的高AE所在的直线翻折,使得点C与BC边上的点D重合.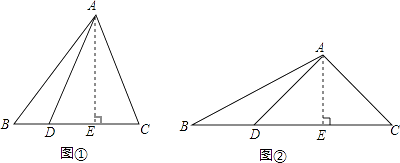
(1)填空:△ADC是三角形;
(2)若AB=15,AC=13,BC=14,求BC边上的高AE的长;
(3)如图②,若∠DAC=90°,试猜想:BC、BD、AE之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若正方形有两个相邻顶点在三角形的同一条边上,其余两个顶点分别在三角形的另两条边上,则正方形称为三角形该边上的内接正方形,△ABC中,设BC=a,AC=b,AB=c,各边上的高分别记为![]() ,
,![]() ,
,![]() ,各边上的内接正方形的边长分别记为
,各边上的内接正方形的边长分别记为![]() ,
,![]() ,
,![]() .
.
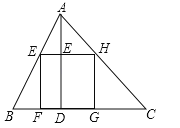
(1)模拟探究:如图,正方形EFGH为△ABC的BC边上的内接正方形,求证:![]() ;
;
(2)特殊应用:若∠BAC=90°,![]() =
=![]() =2,求
=2,求![]() 的值;
的值;
(3)拓展延伸:若△ABC为锐角三角形,b<c,请判断![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;
①求tan∠CFE的值;
②若AC=3,BC=4,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年,中央财政安排资金 8 200 000 000 元,免除城市义务教育学生学杂费,支持进城务工人员随迁子女公平接受义务教育,这个数据用科学记数法可表示为元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com