
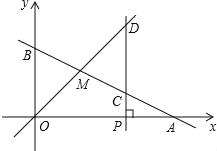
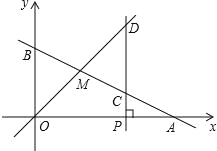
【题目】如图,已知函数y=kx+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点A的坐标为(6,0),点M的横坐标为2,过点P(a,0),作x轴的垂线,分别交函数y=kx+b和y=x的图象于点C、D.
(1)求函数y=kx+b的表达式;
(2)若点M是线段OD的中点,求a的值.
【答案】(1)y=﹣![]() x+3.(2)a=4.
x+3.(2)a=4.
【解析】
试题分析:(1)由点A的横坐标利用一次函数图象上点的坐标特征即可找出点M的坐标,结合点A的坐标利用待定系数法即可求出直线AB的表达式;
(2)由PD⊥x轴可得出PC∥OB,根据平行线的性质可得出∠BOM=∠CDM,结合点M是线段OD的中点以及对顶角相等即可证出△MBO≌△MCD,根据全等三角形的性质即可得出OB=DC,由直线AB的解析式可得出OB的长度,再由点P的坐标即可得出点C、D的坐标,根据OB=DC即可得出关于a的一元一次方程,解方程即可求出a值.
试题解析:(1)∵点M的横坐标为2,点M在直线y=x上,∴y=2,∴点M的坐标为(2,2).
把M(2,2)、A(6,0)代入到y=kx+b中,
得:![]() ,解得:
,解得: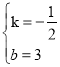 ,∴函数的表达式为y=﹣
,∴函数的表达式为y=﹣![]() x+3.
x+3.
(2)∵PD⊥x轴,∴PC∥OB,∴∠BOM=∠CDM.∵点M是线段OD的中点,
∴MO=MD.
在△MBO≌△MCD中,有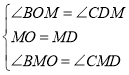 ,∴△MBO≌△MCD(ASA),
,∴△MBO≌△MCD(ASA),
∴OB=DC.
当x=0时,y=﹣![]() x+3=3,∴OB=3,∴DC=3.
x+3=3,∴OB=3,∴DC=3.
当x=a时,y=﹣![]() x+3=﹣
x+3=﹣![]() a+3,y=x=a,
a+3,y=x=a,
∴DC=a﹣(﹣![]() a+3)=
a+3)=![]() a﹣3=3,∴a=4.
a﹣3=3,∴a=4.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
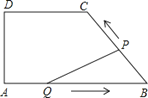
【题目】如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题:
(1)当t为何值时,P,Q两点同时停止运动?
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣1,﹣3)和点B(3,m),且AB平行于x轴,则点B坐标为( )
A. (3,﹣3) B. (3,3) C. (3,1) D. (3,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由一些大小相同,棱长为1的小正方体搭成的几何体的俯视图如图所示,数字表示该位置的正方体个数. 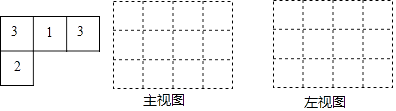
(1)请画出它的主视图和左视图;
(2)给这个几何体喷上颜色(底面不喷色),需要喷色的面积为
(3)在不改变主视图和俯视图的情况下,最多可添加块小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC,其中正确结论的个数为( )
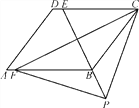
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“母亲节”前期,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销售量大,店主决定将玫瑰每枝降价1元促销,降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍.
(1)求降价后每枝玫瑰的售价是多少元?
(2)根据销售情况,店主用不多于900元的资金再次购进两种鲜花共500枝,康乃馨进价为2元/枝,玫瑰进价为1.5元/枝,问至少购进玫瑰多少枝?
查看答案和解析>>
科目:初中数学 来源: 题型:
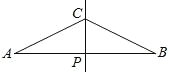
【题目】如图,直线CP是AB的中垂线且交AB于P,其中AP=2CP.甲、乙两人想在AB上取两点D、E,使得AD=DC=CE=EB,其作法如下:
甲:作∠ACP、∠BCP之角平分线,分别交AB于D、E,则D、E即为所求;
乙:作AC、BC之中垂线,分别交AB于D、E,则D、E即为所求.
对于甲、乙两人的作法,下列判断何者正确( )
A. 两人都正确 B. 两人都错误 C. 甲正确,乙错误 D. 甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
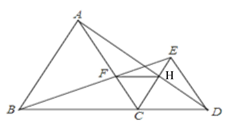
【题目】已知:点B,C,D在同一直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H,
(1)求证:△BCE≌△ACD;
(2)判断△CFH的形状并说明理由.
(3)写出FH与BD的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com