
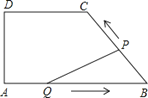
【题目】如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题:
(1)当t为何值时,P,Q两点同时停止运动?
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值.
【答案】(1)、5;(2)、![]() ;(3)、t=
;(3)、t=![]() s,
s,![]() s或t=4s
s或t=4s
【解析】试题分析:(1)、通过比较线段AB,BC的大小,找出较短的线段,根据速度公式可以直接求得;(2)、由已知条件,把△PQB的边QB用含t的代数式表示出来,三角形的高可由相似三角形的性质也用含t的代数式表示出来,代入三角形的面积公式可得到一个二次函数,即可求出S的最值;(3)、根据等腰三角形的性质和余弦公式列出等式求解,即可求的结论.
试题解析:(1)、作CE⊥AB于E, ∵DC∥AB,DA⊥AB, ∴四边形AECD是矩形,
∴AE=CD=5,CE=AD=4, ∴BE=3, ∴BC=5, ∴BC<AB,
∴P到C时,P、Q同时停止运动, ∴t=![]() (秒), 即t=5秒时,P,Q两点同时停止运动.
(秒), 即t=5秒时,P,Q两点同时停止运动.
(2)、由题意知,AQ=BP=t, ∴QB=8﹣t, 作PF⊥QB于F,则△BPF~△BCE,
∴![]() ,即
,即![]() , ∴BF=
, ∴BF=![]() ,
,![]()
∴S=![]() QBPF=
QBPF=![]() ×
×![]() (8﹣t)=﹣
(8﹣t)=﹣![]() (t﹣4)2+
(t﹣4)2+![]() (0<t≤5),
(0<t≤5),
∵﹣![]() <0, ∴S有最大值,当t=4时,S的最大值是
<0, ∴S有最大值,当t=4时,S的最大值是![]() ;
;
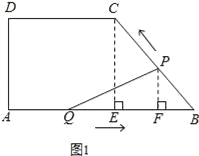
(3)、∵cos∠B=![]() , ①当PQ=PB时(如图2所示),则BG=
, ①当PQ=PB时(如图2所示),则BG=![]() BQ,
BQ,![]() =
=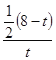 =
=![]() ,解得t=
,解得t=![]() s,
s,
②当PQ=BQ时(如图3所示),则BG=![]() PB,
PB,![]() =
=![]() =
=![]() ,解得t=
,解得t=![]() s,
s,
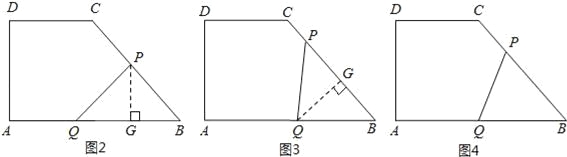
③当BP=BQ时(如图4所示),则8﹣t=t, 解得:t=4.
综上所述:当t=![]() s,
s,![]() s或t=4s时,△PQB为等腰三角形.
s或t=4s时,△PQB为等腰三角形.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】列方程解应用题: 油桶制造厂的某车间主要负责生产制造油桶用的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片120片或者长方形铁片80片.如图,一个油桶由两个圆形铁片和一个长方形铁片相配套.生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据交通运输部统计,受肺炎疫情影响,今年春运1月25日~2月14日,全国共发送旅客2.83亿人次,日均1348万人次,同比分别下降82.3%,将1348万用科学记数法表示为( )
A.1348×104B.13.48×106C.1.348×106D.1.348×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=6cm,MB=10cm,点M,N分别为AC,BC的中点. ![]()
(1)求线段BC,MN的长;
(2)若C在线段AB的延长线上,且满足AC﹣BC=acm,M,N分别是线段AC,BC的中点,请画出图形,并用a的式子表示MN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
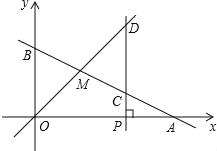
【题目】如图,已知函数y=kx+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点A的坐标为(6,0),点M的横坐标为2,过点P(a,0),作x轴的垂线,分别交函数y=kx+b和y=x的图象于点C、D.
(1)求函数y=kx+b的表达式;
(2)若点M是线段OD的中点,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com