
分析 (1)先移项、然后利用平方差公式分解因式;
(2)(3)利用配方法求解即可.
解答 解:(1)移项得:(3x-1)2-(x+1)2=0,
(3x-1+x+1)(3x-1-x-1)=0
4x(2x-2)=0
∴x1=1,x2=0
(2)移项得:2x2+x=1,
2(${x}^{2}+\frac{1}{2}x+\frac{1}{16}$)=1+$\frac{1}{8}$
∴$(x+\frac{1}{4})^{2}=\frac{9}{16}$.
∴$x+\frac{1}{4}=±\frac{3}{4}$.
∴x1=-1,${x}_{2}=\frac{1}{2}$.
(3)移项得:x2-4x=-1,
方程两边同时加上4得;x2-4x+4=3.
∴(x-2)2=3.
∴$x-2=±\sqrt{3}$.
解得:${x}_{1}=2+\sqrt{3}$,${x}_{2}=2-\sqrt{3}$.
点评 本题主要考查的是解一元二次方程,掌握解一元二次方程的方法是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
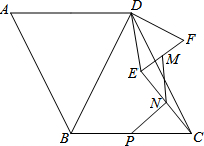 在?ABCD中,∠A=∠DBC,过点D作DE=DF,且∠EDF=∠ABD,连接EF、EC,M、N、P分别为EF、EC、BC的中点,连接NP.请你发现∠ABD与∠MNP满足的等量关系,并证明.
在?ABCD中,∠A=∠DBC,过点D作DE=DF,且∠EDF=∠ABD,连接EF、EC,M、N、P分别为EF、EC、BC的中点,连接NP.请你发现∠ABD与∠MNP满足的等量关系,并证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
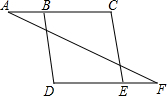 如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.
如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com