
【题目】如图,四边形ABCD是矩形,直线L垂直分线段AC,垂足为O,直线L分别于线段AD,CB的延长线交于点E,F,证明四边形AFCE是菱形.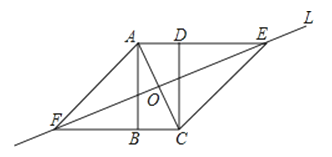
科目:初中数学 来源: 题型:
【题目】计算(-8m4n+12m3n2-4m2n3)÷(-4m2n) 的结果是( )
A. 2m2n-3m+n2 B. 2m2-3nm2+n2
C. 2m2-3mn+n D. 2m2-3mn+n2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市郊外景区内一条笔直的公路a经过三个景点A、B、C,景区管委会又开发了风景优美的景点D,经测量景点D位于景点A的北偏东30°方向8km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上,已知AB=5km.

(1)景区管委会准备由景点D向公路a修建一条距离最短的公路,不考虑其它因素,求出这条公路的长;(结果精确到0.1km)
(2)求景点C与景点D之间的距离.(结果精确到1km)
(参考数据:![]() =1.73,
=1.73,![]() =2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
=2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
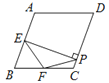
A. 55° B. 50° C. 45° D. 35°
查看答案和解析>>
科目:初中数学 来源: 题型:
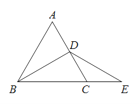
【题目】如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD.
(1)用尺规作图的方法,过点D作DM⊥BE,垂足为M(不写作法,只保留作图痕迹);
(2)若AB=2,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC、BD相交于点O , 已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD;则不能使四边形ABCD成为矩形的是( ).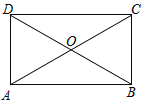
A.①②③
B.②③④
C.②⑤⑥
D.④⑤⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m. 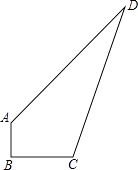
(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣mx﹣2m2=0.
(1)求证:不论m为何值,该方程总有两个实数根;
(2)若x=1是该方程的根,求代数式4m2+2m+5的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com