
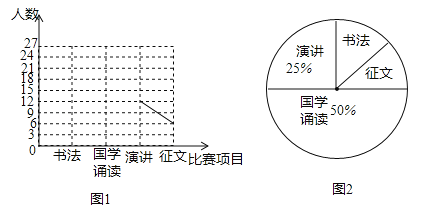
【题目】在图“书香八桂,阅读圆梦”读数活动中,某中学设置了书法、国学、诵读、演讲、征文四个比赛项目(每人只参加一个项目),九(2)班全班同学都参加了比赛,该班班长为了了解本班同学参加各项比赛的情况,收集整理数据后,绘制以下不完整的折线统计图(图1)和扇形统计图(图2),根据图表中的信息解答下列各题:
(1)请求出九(2)全班人数;
(2)请把折线统计图补充完整;
(3)南南和宁宁参加了比赛,请用“列表法”或“画树状图法”求出他们参加的比赛项目相同的概率.
【答案】(1)48;(2)答案见解析;(3)![]() .
.
【解析】
试题分析:(1)由演讲人数12人,占25%,即可求得九(2)全班人数;
(2)首先求得书法与国学诵读人数,继而补全折线统计图;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与他们参加的比赛项目相同的情况,再利用概率公式求解即可求得答案.
试题解析:(1)∵演讲人数12人,占25%,∴出九(2)全班人数为:12÷25%=48(人);
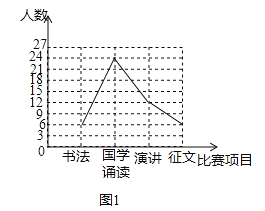
(2)∵国学诵读占50%,∴国学诵读人数为:48×50%=24(人),∴书法人数为:48﹣24﹣12﹣6=6(人);
补全折线统计图;
(3)分别用A,B,C,D表示书法、国学诵读、演讲、征文,画树状图得:
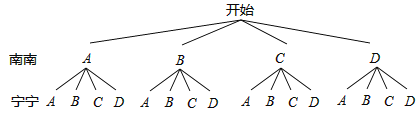
∵共有16种等可能的结果,他们参加的比赛项目相同的有4种情况,∴他们参加的比赛项目相同的概率为:![]() =
=![]() .
.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】足球比赛的积分规则:胜一场得3分,平一场得1分,负一场得0分.一个队进行了14场比赛,其中负5场,共得19分,那么这个对共胜了( )场.
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】泰兴市新区对曾涛路进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完.则原有树苗( )棵.
A.100
B.105
C.106
D.111
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断( )
①年用水量不超过180m3的该市居民家庭按第一档水价交费;
②年用水量超过240m3的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在150﹣180之间;
④该市居民家庭年用水量的平均数不超过180.
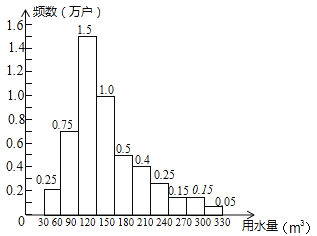
A.①③ B.①④ C.②③ D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定存款利息的纳税办法是:利息税=利息×20%,银行一年定期的利率为2.25%,今小磊取出一年到期的本金及利息时,交纳了4.5元利息税,则小磊一年前存入银行的钱为( )
A.1000元
B.900元
C.800元
D.700元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC. 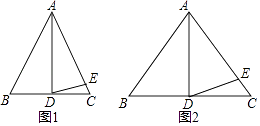
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC= .
(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC= .
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A. (a+b)3=a3+b3 B. 2a3·3a2=6a6
C. (-x3)4=x12 D. (-x)3n÷(-x)2n=-xn
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点O为直线AB上一点,∠COD=90°,射线OE平分∠AOD.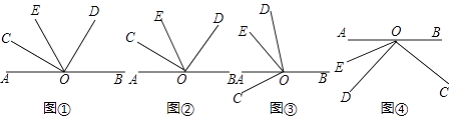
(1)如图①所示,若∠COE=20°,则∠BOD=°.
(2)若将∠COD绕点O旋转至图②的位置,试判断∠BOD和∠COE的数量关系,并说明理由;
(3)若将∠COD绕点O旋转至图③的位置,∠BOD和∠COE的数量关系是否发生变化?并请说明理由.
(4)若将∠COD绕点O旋转至图④的位置,继续探究∠BOD和∠COE的数量关系,请直接写出∠BOD和∠COE之间的数量关系: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com