
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() ,
,![]() 上,连接
上,连接![]() .
.
(1)将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
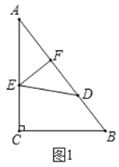
边上的点![]() 处,如图1,若
处,如图1,若![]() ,求
,求![]() 的长;
的长;
(2)将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
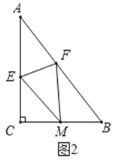
边上的点![]() 处,如图2,若
处,如图2,若![]() .
.
①求![]() 的长;
的长;
②求四边形![]() 的面积;
的面积;
(3)若点![]() 在射线
在射线![]() 上,点
上,点![]() 在边
在边![]() 上,点
上,点![]() 关于
关于![]() 所在直线的对称点为点
所在直线的对称点为点![]() ,问:是否存在以
,问:是否存在以![]() 、
、![]() 为对边的平行四边形,若存在,求出
为对边的平行四边形,若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() ;(3)存在,
;(3)存在,![]() 或6.
或6.
【解析】
(1)先判断出S△ABC=4S△AEF,再求出AB,判断出Rt△AEF∽△Rt△ABC,得出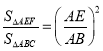 ,代值即可得出结论;
,代值即可得出结论;
(2)先判断出四边形AEMF是菱形,再判断出△CME∽△CBA得出比例式,代值即可得出结论;
(3)分两种情况,利用平行四边形的性质,对边平行且相等,最后用勾股定理即可得出结论.
解:(1)∵![]() 沿
沿![]() 折叠,折叠后点
折叠,折叠后点![]() 落在
落在![]() 上的点
上的点![]() 处,
处,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,∵
中,∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴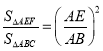 ,
,
即:![]() ,
,
∴![]() ;
;
(2)①∵![]() 沿
沿![]() 折叠,折叠后点
折叠,折叠后点![]() 落在
落在![]() 边上的点
边上的点![]() 处,
处,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是菱形,
是菱形,
设![]() ,则
,则![]() ,
,![]() ,
,
∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
即:![]() ,
,
②由①知,![]() ,
,![]() ,
,
∴![]() ;
;
(3)①如图3,当点![]() 在线段
在线段![]() 上时,
上时,
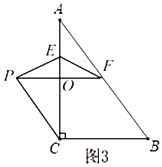
∵![]() 与
与![]() 是平行四边形的对边,
是平行四边形的对边,
∴![]() ,
,![]() ,
,
由对称性知,![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∴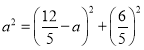 ,
,
∴![]() ,
,
即:![]() ;
;
②如图4,当点![]() 在线段
在线段![]() 的延长线上时,延长
的延长线上时,延长![]() 交
交![]() 于
于![]() ,
,
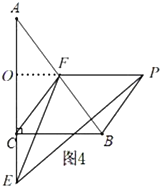
同理:![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∴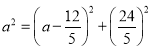 ,
,
∴![]() ,
,
∴![]() ,
,
即:![]() 或6.
或6.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】数轴上点A,B,C的位置如图,点C是线段AB的中点,点A表示的数比点C表示的数的两倍还大3,点B和点C表示的数是互为相反数,点C表示的数是__________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的《朗读者》节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数量少的有![]() 本,最多的有
本,最多的有![]() 本,并根据调查结果绘制了不完整的图表,如下所示:
本,并根据调查结果绘制了不完整的图表,如下所示:
本数(本) | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|

(![]() )统计图表中的
)统计图表中的![]() __________,
__________,![]() __________,
__________,![]() __________.
__________.
(![]() )请将频数分布直方图补充完整.
)请将频数分布直方图补充完整.
(![]() )求所有被调查学生课外阅读的平均本数.
)求所有被调查学生课外阅读的平均本数.
(![]() )若该校八年级共有
)若该校八年级共有![]() 名学生,请你估计该校八年级学生课外阅读
名学生,请你估计该校八年级学生课外阅读![]() 本及以上的人数.
本及以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为A(100﹣90分)、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下问题:
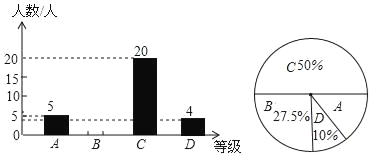
(1)这次随机抽取的学生共有多少人?
(2)请补全条形统计图;
(3)这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOC与∠BOD具有公共顶点,∠COD是两个角叠合的部分.
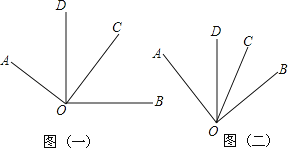
(1)若∠AOC=∠BOD=90°,观察图形(一)并完成下列问题:
①直接写出图中两个相等的锐角: = ;
②如果∠COD=40°,则∠AOB= ,若∠AOB=150°,则∠COD= ;
③猜想∠AOB+∠DOC= °,请说明理由.
(2)探究图形(二):若∠AOC=60°,∠BOD=50°,则∠AOB+∠DOC= °,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy 中,点A 的坐标为(1,0),P 是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).若点P到x轴的距离为![]() ,则m+n 的最小值为___.
,则m+n 的最小值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校八年级150名女生的身高情况,从中随机抽取10名女生,测得身高并绘制如下条形统计图.
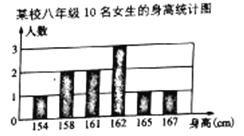
(1)求出这10名女生的身高的中位数和众数;
(2)依据样本估计该校八年级全体女生的平均身高;
(3)请你根据这个样本,在该校八年级中,设计一个挑选50名女生组成方队的方案(要求选中女生的身高尽可能接近).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com