
 如图,∠ACB=∠AED=90°,AC=BC,AD平分∠BAC交BC于点D,若AB=9,则△DEB的周长为
如图,∠ACB=∠AED=90°,AC=BC,AD平分∠BAC交BC于点D,若AB=9,则△DEB的周长为
|


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
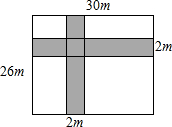 邻居李大叔在自家后院种了一块长30m,宽26m的长方形菜地,为行走方便,准备修筑两条横竖方向互相垂直的小路如图所示,路宽2m,请你帮助计算一下种植蔬菜的面积.
邻居李大叔在自家后院种了一块长30m,宽26m的长方形菜地,为行走方便,准备修筑两条横竖方向互相垂直的小路如图所示,路宽2m,请你帮助计算一下种植蔬菜的面积.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
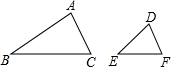 如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,△ABC的面积是24,则△DEF的面积为( )
如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,△ABC的面积是24,则△DEF的面积为( )A、2
| ||
| B、6 | ||
| C、12 | ||
| D、48 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com