
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据一次函数、反比例函数、二次函数的增减性对各小题分析判断后利用排除法求解.
解答 解:①y=-$\frac{1}{2x}$,在每一象限内y随x的增大而增大,故本小题错误;
②y=-1+$\frac{1}{2}$x中y随x的增大而增大,故本小题正确;
③y=-x2+2x+3(x>2),对称轴为直线x=-$\frac{2}{2×(-1)}$=1,
x<1时,y随x的增大而增大,故本小题正确;
④y=-2x中y随着x的增大而减小,故本小题错误;
只有②③y的值随着x的增大而增大.
故选B.
点评 本题考查了二次函数的增减性,一次函数、反比例函数的增减性,特别注意,反比例函数的增减性必须强调在每一个象限内.


科目:初中数学 来源: 题型:解答题
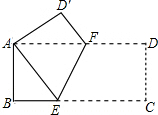 如图,将矩形ABCD折叠,使点C与A点重合,折痕为EF.
如图,将矩形ABCD折叠,使点C与A点重合,折痕为EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,四边形ABCD是梯形,AD∥BC,E是BC的中点,BC=12,点A坐标是(0,4),CD所在直线的函数关系式为y=-x+9,点P是BC边上一个动点,
如图,在平面直角坐标系中,四边形ABCD是梯形,AD∥BC,E是BC的中点,BC=12,点A坐标是(0,4),CD所在直线的函数关系式为y=-x+9,点P是BC边上一个动点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
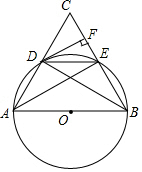 如图,AB为⊙O的直径,点C为圆外一点,连接AC、BC,分别与⊙O相交于点D、点E,且$\widehat{AD}$=$\widehat{DE}$,过点D作DF⊥BC于点F,连接BD、DE、AE.
如图,AB为⊙O的直径,点C为圆外一点,连接AC、BC,分别与⊙O相交于点D、点E,且$\widehat{AD}$=$\widehat{DE}$,过点D作DF⊥BC于点F,连接BD、DE、AE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | 1 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
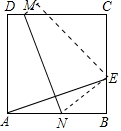 如图,在正方形ABCD中,E是BC的中点,折叠正方形使点A与E重合,折痕为MN,若梯形ADMN的面积是$\frac{3}{2}$,则正方形的边长是2;梯形ADMN与梯形BCMN的面积之比是$\frac{3}{5}$.
如图,在正方形ABCD中,E是BC的中点,折叠正方形使点A与E重合,折痕为MN,若梯形ADMN的面积是$\frac{3}{2}$,则正方形的边长是2;梯形ADMN与梯形BCMN的面积之比是$\frac{3}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com