
【题目】(1)化简![]() ;
;
(2)若n=![]() ,求①n2-2n; ②4n3﹣9n2﹣2n+1; ③ 3n2﹣7n+
,求①n2-2n; ②4n3﹣9n2﹣2n+1; ③ 3n2﹣7n+![]() +4的值.
+4的值.
【答案】(1)2;(2)①1;②0;③5
【解析】
(1)原式各项进行分母有理化,计算即可得解;
(2)将所给条件进行分母有理化后,再把所求代数式分别进行变形后代入求值即可.
(1)![]() +
+![]() +…+
+…+![]()
=![]() ﹣1+
﹣1+![]() ﹣
﹣![]() +2﹣
+2﹣![]() +…+3﹣2
+…+3﹣2![]()
=2;
(2)∵n=![]() ,
,
∴n=![]() +1, 则n﹣1=
+1, 则n﹣1=![]() ,
,
①n2-2n =n2-2n +1-1=(n-1)2-1=2-1=1;
②4n3﹣9n2﹣2n+1 =n(4n2﹣8n)﹣n2﹣2n+1
=4n﹣n2﹣2n+1
=﹣(n2﹣2n)+1
=﹣(n﹣1)2+2
=﹣(![]() +1﹣1)2+2
+1﹣1)2+2
=0;
③3n2﹣7n+![]() +4 =3(
+4 =3(![]() +1)2﹣7(
+1)2﹣7(![]() +1)+
+1)+![]() ﹣1+4
﹣1+4
=3(3+2![]() )﹣7
)﹣7![]() ﹣7+
﹣7+![]() +3
+3
=5.


科目:初中数学 来源: 题型:
【题目】如图,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论不正确的结论是( )

A.CD=DN;B.∠1=∠2;C.BE=CF;D.△ACN≌△ABM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.

(1)如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,请写出图中两对“等角三角形”.
(2)如图2,在△ABC中,CD为角平分线,∠A=40°,∠B=60°。求证:CD为△ABC的等角分割线.
(3)在△ABC中,∠A=42°,CD是△ABC的等角分割线,若△ACD是等腰三角形,请直接写出∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地民政局计划将批物资运往灾区,在这批物资中,帐篷和食品共320件,帐篷比食品多80件.
(1)求帐篷和食品各多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这些物资全部运往灾区,已知甲型货车最多可装帐篷40件和食品10件;乙种货车最多可装帐篷和食品各20件,计算说明安排甲、乙两种货车有几种方案?
(3)在(2)的条件下,甲种货车每辆需付运费4000元,乙种货车每辆需付运费3600元,民政局应选择哪种运输方案,才能使运输费用最少?最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.试判断线段AB与DE的数量关系和位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 于D,且
于D,且![]() ,以AB为底边作等腰直角三角形ABE,连接ED、EC,延长CE交AD于点F,下列结论:①
,以AB为底边作等腰直角三角形ABE,连接ED、EC,延长CE交AD于点F,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的有( ).
,其中正确的有( ).

A.①②B.①③C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB于点E,DF⊥BC于点F.将∠EDF以点D为旋转中心旋转,其两边DE′,DF′分别与直线AB,BC相交于点G,P,连接GP,当△DGP的面积等于3![]() 时,求旋转角的大小并指明旋转方向.
时,求旋转角的大小并指明旋转方向.
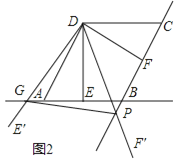
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com