
【题目】如图,在![]() 中,
中,![]() 于D,且
于D,且![]() ,以AB为底边作等腰直角三角形ABE,连接ED、EC,延长CE交AD于点F,下列结论:①
,以AB为底边作等腰直角三角形ABE,连接ED、EC,延长CE交AD于点F,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的有( ).
,其中正确的有( ).

A.①②B.①③C.①②③D.①②③④
【答案】D
【解析】
①易证∠CBE=∠DAE,用SAS即可求证:△ADE≌△BCE;②根据①结论可得∠AEC=∠DEB,即可求得∠AED=∠BEG,即可解题;③证明△AEF≌△BED即可;④易证△FDC是等腰直角三角形,则CE=EF,S△AEF=S△ACE,由△AEF≌△BED,可知S△BDE=S△ACE,所以S△BDE=S△ACE.
解:∵AD为△ABC的高线
∴∠CBE+∠ABE+∠BAD=90°,
∵Rt△ABE是等腰直角三角形,
∴∠ABE=∠BAE=∠BAD+∠DAE=45°,AE=BE,
∴∠CBE+∠BAD=45°,
∴∠DAE=∠CBE,
在△DAE和△CBE中,
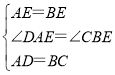
∴△ADE≌△BCE(SAS);
故①正确;
∵△ADE≌△BCE,
∴∠EDA=∠ECB,AD=BC,DE=EC,
∵∠ADE+∠EDC=90°,
∴∠EDC+∠ECB=90°,
∴∠DEC=90°,
∴CE⊥DE,△DEC是等腰直角三角形,易证△DFC是等腰直角三角形,
故③正确,
∴DF=DC,
∵BC=BD+DC=BD+DF=AD,
故②正确;
∵AD=BC,BD=AF,
∴CD=DF,
∵AD⊥BC,
∴△FDC是等腰直角三角形,
∵DE⊥CE,
∴EF=CE,
∴S△AEF=S△ACE,
∵△AEF≌△BED,
∴S△AEF=S△BED,
∴S△BDE=S△ACE.
故④正确;
故选:D.


科目:初中数学 来源: 题型:
【题目】某中学对九年级准备选考1分钟跳绳的同学进行测试,测试结果如下表:
频数分布表:
组别 | 跳绳(次/1分钟) | 频数 |
第1组 | 190~199 | 5 |
第2组 | 180~189 | 11 |
第3组 | 170~179 | 23 |
第4组 | 160~169 | 33 |
请回答下列问题:
(1)此次测试成绩的中位数落在第 组中;
(2)如果成绩达到或超过180次/分钟的同学可获满分,那么本次测试中获得满分的人数占参加测试人数的 %;
(3)如果该校九年级参加体育测试的总人数为200人,若要绘制一张统计该校各项目选考人数分布的扇形图(如图),图中A所在的扇形表示参加选考1分钟跳绳的人数占测试总人数的百分比,那么该扇形的圆心角应为 °;
(4)如果此次测试的平均成绩为171次/分钟,那么这个成绩是否可用来估计该校九年级学生跳绳的平均水平?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级学生一学期参加公益活动的时间情况,抽取50名八年级学生为样本进行调查,按参加公益活动的时间t(单位:小时),将样本分成五类:A类(0≤t≤2),B类(2<t≤4),C类(4<t≤6),D类(6<t≤8),E类(t>8),绘制成尚不完整的条形统计图.
(1)样本中,E类学生有 人,请补全条形统计图;
(2)该校八年级共600名学生,求八年级参加公益活动时间6<t≤8的学生数;
(3)从样本中选取参加公益活动时间在0≤t≤4的2人做志愿者,求这2人参加公益活动时间都在2<t≤4中的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次研究性学习活动中,同学们看到了工人师傅在木板上画一个直角三角形的过程(如图所示):画线段AB,过点A任作一条直线l,以点A为圆心,以AB长为半径画弧,与直线l相交于两点C、D,连接BC和BD.则△BCD就是直角三角形.
(1)请你说明△BCD是直角三角形的道理;
(2)请利用上述方法作一个直角三角形,使其中一个锐角为60°(不写作法,保留作图
痕迹,在图中注明60°的角).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.

(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划选购甲、乙两种图书作为“校园读书节”的奖品.已知甲图书的单价是乙图书单价的![]() 倍;用
倍;用![]() 元单独购买甲种图书比单独购买乙种图书要少
元单独购买甲种图书比单独购买乙种图书要少![]() 本.
本.
(1)甲、乙两种图书的单价分别为多少元?
(2)若学校计划购买这两种图书共![]() 本,且投入的经费不超过
本,且投入的经费不超过![]() 元,要使购买的甲种图书数量不少于乙种图书的数量,则共有几种购买方案?
元,要使购买的甲种图书数量不少于乙种图书的数量,则共有几种购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com