
 在平面直角坐标系中.
在平面直角坐标系中.分析 (1)取A(0,0),B(2,0),C(2,3),D(0,3),再描点可得到四边形ABCD;
(2)先根据题意写出点A′、B′、C′、D′的坐标,然后描点得到四边形A′B′C′D′;
(3)利用位似的性质,画出四边形ABCD在位似中心同旁的位似图形,于是可得到四边形A′B′C′D′是四边形ABCD的位似图形.
解答 解:(1)如图,四边形ABCD为所作;
(2)如图,四边形A′B′C′D′为所作;
(3)以坐标原点为位似中心,把四边形ABCD按相似比2:1放大可得到四边形A′B′C′D′,
所以四边形ABCD按相似比2:1放大的四边形的各顶点的横坐标、纵坐标分别是四边形ABCD各顶点的横坐标、纵坐标的2倍或-2倍.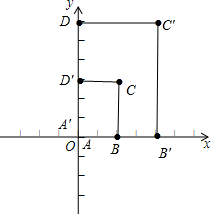
点评 本题考查了作图-位似变换:先确定位似中心;再分别连接并延长位似中心和能代表原图的关键点;接着根据位似比,确定能代表所作的位似图形的关键点;然后顺次连接上述各点,得到放大或缩小的图形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
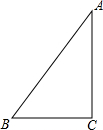 某年某地地震造成了大量的山体滑坡,其中有一处长为60米的滑坡覆盖了整条公路,使原来平坦的公路成了与山坡浑然一体的斜坡,如图的直角三角形ABC是塌方的横截面,为了及时清除这路段上的塌方,必须马上估计塌方的数量.工程兵测得原来公路的宽BC=12米,坡角∠ABC=60°,如果采用一台每小时可清除100立方米的挖掘机,全部清理完这个路段需要多少小时?(精确到1小时)
某年某地地震造成了大量的山体滑坡,其中有一处长为60米的滑坡覆盖了整条公路,使原来平坦的公路成了与山坡浑然一体的斜坡,如图的直角三角形ABC是塌方的横截面,为了及时清除这路段上的塌方,必须马上估计塌方的数量.工程兵测得原来公路的宽BC=12米,坡角∠ABC=60°,如果采用一台每小时可清除100立方米的挖掘机,全部清理完这个路段需要多少小时?(精确到1小时)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
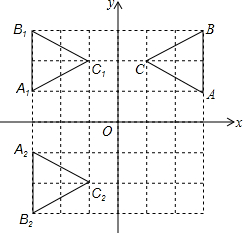 如图,在平面直角坐标系中,△ABC为等边三角形,其中点A,B,C的坐标分别为(3,1),(3,3),(3-$\sqrt{3}$,2),现以y轴为对称轴作△ABC的对称图形得△A1B1C1,再以x轴为对称轴作的对称图形,得△A2B2C2.
如图,在平面直角坐标系中,△ABC为等边三角形,其中点A,B,C的坐标分别为(3,1),(3,3),(3-$\sqrt{3}$,2),现以y轴为对称轴作△ABC的对称图形得△A1B1C1,再以x轴为对称轴作的对称图形,得△A2B2C2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
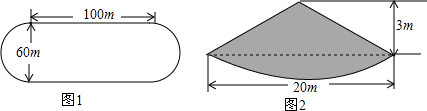
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com