
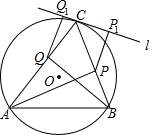
 如图,过△ABC的顶点C作这个三角形的外接圆的切线l,AP和BQ即是△ABC的两条高,QQ1⊥l,PP1⊥l,求证:QQ1=PP1.
如图,过△ABC的顶点C作这个三角形的外接圆的切线l,AP和BQ即是△ABC的两条高,QQ1⊥l,PP1⊥l,求证:QQ1=PP1. 分析 作辅助线,构建四边形QPP1Q1和直径,只要证明四边形QPP1Q1为矩形就可以得出结论,由图形和已知发现四边形QPP1Q1有两个角是直角,只要再证明一个直角即可,所以本题的重点是证明∠QPP1=90°即可.
解答 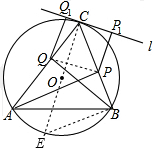 证明:连接CO,并延长交⊙O于E,连接BE、PQ,
证明:连接CO,并延长交⊙O于E,连接BE、PQ,
∵AP和BQ是△ABC的两条高,
∴AP⊥BC,BQ⊥AC,
∴∠APB=∠AQB=90°,
∴A、B、P、Q四点共圆,
∴∠QPC=∠CAB,
∵∠CAB=∠E,
∴∠E=∠QPC,
∵l是⊙O的切线,
∴EC⊥l,
∵PP1⊥l,
∴PP1∥EC,
∴∠ECB=∠CPP1,
∵EC为⊙O的直径,
∴∠EBC=90°,
∴∠E+∠ECB=90°,
∴∠QPC+∠CPP1=90°,
即∠QPP1=90°,
∵QQ1⊥l,PP1⊥l,
∴∠QQ1C=∠PP1C=90°,
∴四边形QPP1Q1为矩形,
∴QQ1=PP1.
点评 本题考查了切线的性质、圆周角定理、矩形的性质和判定以及四点共圆的判定和性质,本题的关键是证明∠QPP1=90°即可;要熟练掌握矩形的判定和四点共圆的判定.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
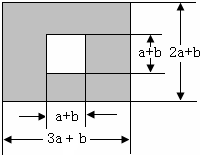 如图,某校有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,学校计划将阴影部分进行绿化,中间将修建一座雕像.
如图,某校有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,学校计划将阴影部分进行绿化,中间将修建一座雕像.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
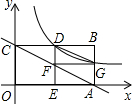 如图,已知矩形OABC中,点A(2,0)、C(0,1).点D是边BC的中点,过点D作DE⊥OA于点E,双曲线y=$\frac{k}{x}$过点D交AB于点G,直线AC交DE于点F,连接DG、FG.
如图,已知矩形OABC中,点A(2,0)、C(0,1).点D是边BC的中点,过点D作DE⊥OA于点E,双曲线y=$\frac{k}{x}$过点D交AB于点G,直线AC交DE于点F,连接DG、FG.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
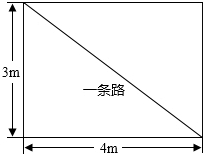 在“寻找滨河最美,拒绝不文明行为”系列活动中,细心的董明同学发现:学校六号楼前有一块长方形花圃(如图所示),有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,请你计算,他们仅仅少走了4步路(假设2步为1米),却踩伤了花草.
在“寻找滨河最美,拒绝不文明行为”系列活动中,细心的董明同学发现:学校六号楼前有一块长方形花圃(如图所示),有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,请你计算,他们仅仅少走了4步路(假设2步为1米),却踩伤了花草.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com