
分析 观察已知算式可以发现:等式左侧乘积的第一个因数是从1开始的连续自然数,第二个因数的分子和这个自然数相同,分母比分子大1;右侧恰是左侧两个因数的差;由此可以解决(1)和(2);
(3)根据(2)中算式左侧和右侧进行分式运算比较即可.
解答 解:等式左侧乘积的第一个因数是从1开始的连续自然数,第二个因数的分子和这个自然数相同,分母比分子大1;右侧恰是左侧两个因数的差;
(1)第4个等式:4×$\frac{4}{5}$=4-$\frac{4}{5}$,
(2)第n个等式:n×$\frac{n}{n+1}$=n-$\frac{n}{n+1}$,
(3)证明:n×$\frac{n}{n+1}$=$\frac{{n}^{2}}{n+1}$,n-$\frac{n}{n+1}$=$\frac{n(n+1){-n}^{2}}{n+1}$=$\frac{{n}^{2}}{n+1}$,
∴n×$\frac{n}{n+1}$=n-$\frac{n}{n+1}$,
∴(2)中猜想的结论是正确的.
点评 此题主要考察运算规律的探索应用与证明,观察已知算式找出规律是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
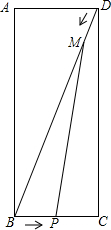 如图所示,在矩形ABCD中.AB=12,BC=5,点P从点B沿BC边向点C运动,点M从点D沿对角线DB向点B运动,且始终保持BP=DM.若设BP=x,△BPM的面积为y,请写出y与x之间的函数关系式,并注明自变量x的取值范围.
如图所示,在矩形ABCD中.AB=12,BC=5,点P从点B沿BC边向点C运动,点M从点D沿对角线DB向点B运动,且始终保持BP=DM.若设BP=x,△BPM的面积为y,请写出y与x之间的函数关系式,并注明自变量x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 92.59×106 | B. | 9.259×107 | C. | 9259×104 | D. | 9.259×106 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com