
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).
请回答:BC+DE的值为
参考小明思考问题的方法,解决问题:
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数
【答案】![]() ;60°
;60°
【解析】解:∵DE∥BC,EF∥DC,
∴四边形DCFE是平行四边形,
∴EF=CD=3,CF=DE,
∵CD⊥BE,
∴EF⊥BE,
∴BC+DE=BC+CF=BF=![]() =
=![]() =
=![]() ;
;
所以答案是:![]() ;
;
解决问题:连接AE,CE,如图.
∵四边形ABCD是平行四边形,
∴AB∥DC.
∵四边形ABEF是矩形,
∴AB∥FE,BF=AE.
∴DC∥FE.
∴四边形DCEF是平行四边形.
∴CE∥DF.
∵AC=BF=DF,
∴AC=AE=CE.
∴△ACE是等边三角形.
∴∠ACE=60°.
∵CE∥DF,
∴∠AGF=∠ACE=60°.
所以答案是:60°
【考点精析】根据题目的已知条件,利用平行四边形的判定与性质的相关知识可以得到问题的答案,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


科目:初中数学 来源: 题型:
【题目】某次考试中,某班级的数学成绩被绘制成了如图所示的频数分布直方图.下列说法错误的是( )

A. 得分在70~80分之间的人数最多 B. 该班的总人数为40
C. 得分在90~100分之间的人数占总人数的5% D. 及格(不低于60分)的人数为26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若t是一元二次方程x2+bx+c=0的根,则判别式△=b2﹣4c和完全平方式M=(2t+b)2的关系是( )
A.△=MB.△>M
C.△<MD.大小关系不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的4月23日是世界读书日,茗茗想了解她所在学校八年级学生课外阅读的喜好,从八年级随机抽取部分学生进行调查,并将调查结果绘制成如图所示的局行统计图,调查要求每人只选取一种喜好的书籍.若选择“漫画”的学生有60人,选择“其他”的学生有30人,则下列说法中不正确的是( )

A. 选择“科普”的学生有90人 B. 该调查的样本容量为300
C. 不能确定选择“小说”的人数 D. “漫画”所在扇形圆心角的度数为72°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,如果当x>0时,函数y=kx﹣1(k≠0)图象上的点都在直线y=﹣1上方,请写出一个符合条件的函数y=kx﹣1(k≠0)的表达式:____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C,且B(1,0),C(0,3),将△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.
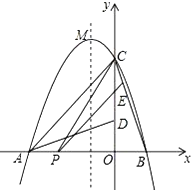
(1)求该二次函数的解析式;
(2)若点P为线段AB上的任一动点,过点P作PE∥AC,交BC于点E,连结CP,求△PCE面积S的最大值;
(3)设抛物线的顶点为M,Q为它的图象上的任一动点,若△OMQ为以OM为底的等腰三角形,求Q点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com