
ij�̳���װ������һ�����Ƴ�����ƽ��ÿ����۳�20����ÿ��ӯ��40Ԫ��Ϊ���������ۣ��̳������������ۣ������飬ÿ����������1Ԫʱ��ƽ��ÿ��ɶ�����2����
��1����ÿ����������xԪ���̳���װ��ÿ��ӯ��yԪ�������y��x֮��ĺ�����ϵʽ��
��2�����̳�ÿ��Ҫӯ��1200Ԫ��ÿ������Ӧ���۶���Ԫ��
��3����ÿ���������۶���Ԫʱ���̳�ÿ���ӯ���ﵽ������ӯ���Ƕ���Ԫ��
��
�����㡿���κ�����Ӧ�ã�
��ר�⡿�������⣮
����������1����ÿ����xԪ����ʾ�����ۺ��ӯ�������۵�������Ȼ�����ÿ���ӯ������ÿ��ӯ�������������ó�y��x�ĺ�����ϵ���ɣ�
��2����y=1200�����ݣ�1���ĺ�����ϵ����Ա�����ȡֵ���ɣ�
��3�������䷽��������κ�������ֵ�������ó��𰸣�
����𡿽⣺��1����ÿ����xԪ���̳�ƽ��ÿ��Ӯ��yԪ��
��y=��40��x����20+2x��=��2x 2+60x+800��
��2����y=1200��
1200=��2��x��15��2+1250��
���x1=10��x2=20��
��ΪΪ���������ۣ����ԣ�Ӧ����20Ԫ��
���̳�ÿ��ƽ����ӯ��1200Ԫ��ÿ������Ӧ����20Ԫ��
��3��y=��2x 2+60x+800��
=��2��x��15��2+1250��
��x=15ʱ��y�����ֵΪ1250Ԫ��
��ÿ������15Ԫʱ���̳�ƽ��ÿ��ӯ����࣮
�����������⿼���˶��κ�����Ӧ���Լ����κ�������ֵ���⣬��ʾ�����ۺ��ӯ�������۵�������Ȼ��õ�ƽ��ÿ���ӯ���뽵��֮��ĺ�����ϵʽ�ǽ���Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
Ϊ�˹���һ���ƶ���������С��������ƶ���ȡ��50��Ⱦɫ�������У�ʹ��Щ�ƶ���ֻ��Ⱥ����ץ��1000���ƶ���������10���ƶ���Ⱦɫ��������ƶ�������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�����г������������¼�������¼����ǣ�������
A��ˮ������ B������¥�� C��������� D��������
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��ۣ�
��a��bͬ�ţ�
�ڵ�x=1��x=3ʱ������ֵ��ȣ�
��4a+b=0��
�ܵ���1��x��5ʱ��y��0��
������ȷ���У�������
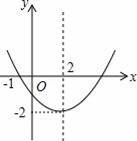

A��1�� B��2�� C��3�� D��4��
��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����֪����y1= ��y2=
��y2=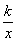 �ڵ�һ����ͼ������y1=
�ڵ�һ����ͼ������y1= ��ͼ���ϵ�����
��ͼ���ϵ�����
һ��A��x���ƽ���߽�����y2=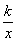 ��ͼ���ڵ�B����y���ڵ�C������AOB�����
��ͼ���ڵ�B����y���ڵ�C������AOB�����
S=l,��k��ֵΪ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com