Question

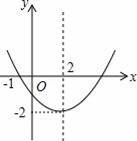
已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，有下列结论：

①a、b同号；

②当x=1和x=3时，函数值相等；

③4a+b=0；

④当﹣1＜x＜5时，y＜0．

其中正确的有（　　）

A．1个  B．2个   C．3个  D．4个

　

　

Answer 1

C【考点】二次函数图象与系数的关系．

【分析】根据函数图象可得各系数的关系：a＞0，b＞0，即可判断①，根据对称轴为x=2，即可判断②；由对称轴x=﹣=2，即可判断③；求得抛物线的另一个交点即可判断④．

【解答】解：∵抛物线开口向下，

∴a＜0，

∵对称轴x=2，

∴﹣=2，

∴b=﹣4a＞0，

∴a、b异号，故①错误；

∵对称轴x=2，

∴x=1和x=3时，函数值相等，故②正确；

∵对称轴x=2，

∴﹣=2，

∴b=﹣4a，

∴4a+b=0，故③正确；

∵抛物线与x轴交于（﹣1，0），对称轴为x=2，

∴抛物线与x轴的另一个交点为（5，0），

∴当﹣1＜x＜5时，y＜0，故④正确；

故正确的结论为②③④三个，

故选C．

【点评】本题考查了二次函数图象与系数的关系：二次函数y=ax²+bx+c（a≠0），二次项系数a决定抛物线的开口方向和大小，当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b和二次项系数a共同决定对称轴的位置，当a与b同号时（即ab＞0），对称轴在y轴左； 当a与b异号时（即ab＜0），对称轴在y轴右；常数项c决定抛物线与y轴交点． 抛物线与y轴交于（0，c）；抛物线与x轴交点个数由△决定，△=b²﹣4ac＞0时，抛物线与x轴有2个交点；△=b²﹣4ac=0时，抛物线与x轴有1个交点；△=b²﹣4ac＜0时，抛物线与x轴没有交点．