
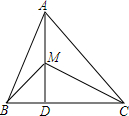
 如图,已知△ABC中,AB=5,AC=7,AD⊥BC于点D,点M为AD上任意一点,则MC2-MB2等于24.
如图,已知△ABC中,AB=5,AC=7,AD⊥BC于点D,点M为AD上任意一点,则MC2-MB2等于24. 分析 在Rt△ABD及RtADC中可分别表示出BD2及CD2,在Rt△BDM及RtCDM中分别将BD2及CD2的表示形式代入表示出BM2和MC2,然后作差即可得出结果.
解答 解:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD和Rt△ADC中,
BD2=AB2-AD2,CD2=AC2-AD2,
在Rt△BDM和Rt△CDM中,
BM2=BD2+MD2=AB2-AD2+MD2,MC2=CD2+MD2=AC2-AD2+MD2,
∴MC2-MB2=(AC2-AD2+MD2)-(AB2-AD2+MD2)
=AC2-AB2
=72-52
=24.
故答案为:24.
点评 本题考查了勾股定理的知识,题目有一定的技巧性,比较新颖,解答本题需要认真观察,分别两次运用勾股定理求出MC2和MB2是本题的难点,重点还是在于勾股定理的熟练掌握.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
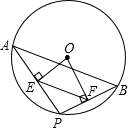 如图,AB是⊙O的弦,点P是⊙O上的动点(P与A、B不重合)连接AP,BP,过点O分别作OE⊥AP于点E,OF⊥PB于点F,试猜想在运动过程中,EF与AB具有怎样的关系,并说明理由.
如图,AB是⊙O的弦,点P是⊙O上的动点(P与A、B不重合)连接AP,BP,过点O分别作OE⊥AP于点E,OF⊥PB于点F,试猜想在运动过程中,EF与AB具有怎样的关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
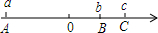 如图,有理数a、b、c在数轴上分别对应点A、B、C点O为原点.
如图,有理数a、b、c在数轴上分别对应点A、B、C点O为原点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com