
【题目】如图,矩形ABCD中,AD=10,AB=8,点E为边DC上一动点,连接AE,把△ADE沿AE折叠,使点D落在点D′处,当△DD′C是直角三角形时,DE的长为 . 
【答案】4或5
【解析】解:∵△ADE沿AE折叠,使点D落在点D′处, ∴DE=D′E,AD=AD′=10,
当∠DD′C=90°时,如图1,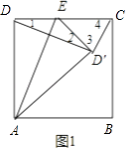
∵DE=D′E,
∴∠1=∠2,
∵∠1+∠4=90°,∠2+∠3=90°,
∴∠3=∠4,
∴ED′=EC,
∴DE=EC= ![]() CD=4;
CD=4;
当∠DCD′=90°时,则点D′落在BC上,如图2,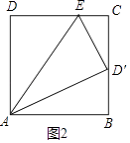
设DE=x,则ED′=x,CE=8﹣x,
∵AD′=AD=10,
∴在Rt△ABD′中,BD′= ![]() =6,
=6,
∴CD′=4,
在Rt△CED′中,(8﹣x)2+42=x2 , 解得x=5,
即DE的长为5,
综上所述,当△DD′C是直角三角形时,DE的长为4或5.
所以答案是4或5.
【考点精析】利用矩形的性质和翻折变换(折叠问题)对题目进行判断即可得到答案,需要熟知矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
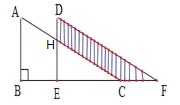
【题目】如图,将Rt△ABC沿射线BC方向平移得到△DEF,已知AB=16cm,BE=10cm,DH=6cm,则图中阴影部分的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
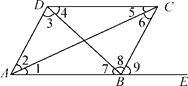
【题目】如图,(1)指出DC和AB被AC所截得的内错角;
(2)指出AD和BC被AE所截得的同位角;
(3)指出∠4与∠7,∠2与∠6,∠ADC与∠DAB各是什么关系的角,并指出各是哪两条直线被哪一条直线所截形成的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A,B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植A类蔬菜面积 | 种植B类蔬菜面积 | 总收入 |
甲 | 3 | 1 | 12500 |
乙 | 2 | 3 | 16500 |
说明:不同种植户种植的同类蔬菜每亩的平均收入相等;亩为土地面积单位.
(1)求A、B两类蔬菜每亩的平均收入各是多少元;
(2)某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由
∵∠1=∠2,∠2=∠3 ,∠1=∠4( )
∴∠3=∠4( )
∴________∥_______ ( )
∴∠C=∠ABD( )
∵∠C=∠D( )
∴∠D=∠ABD( )
∴DF∥AC( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现要把192吨物资从我市运往甲、乙两地,用大、小两种货车共18辆恰好能一次性运完这批物资.已知这两种货车的载重量分别为14吨/辆和8吨/辆,运往甲、乙两地的运费如表:
运往地 | 甲地(元/辆) | 乙地(元/辆) |
大货车 | 720 | 800 |
小货车 | 500 | 650 |
(1)求这两种货车各用多少辆?
(2)如果安排10辆货车前往甲地,其余货车前往乙地,其中前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式;
(3)在(2)的条件下,若运往甲地的物资部少于96吨,请你设计出使总运费最低的货车调配方案,并求出最少总运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
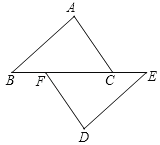
【题目】如图,点B、F、C、E在同一条直线上,点A、D在直线BC的异侧,AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)若∠BFD=150°,求∠ACB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com