
【题目】如图,(1)指出DC和AB被AC所截得的内错角;
(2)指出AD和BC被AE所截得的同位角;
(3)指出∠4与∠7,∠2与∠6,∠ADC与∠DAB各是什么关系的角,并指出各是哪两条直线被哪一条直线所截形成的.
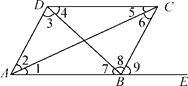
【答案】(1)∠1和∠5;(2)∠DAB和∠9;(3)∠4和∠7是内错角,是直线DC和AB被DB所截形成的;∠2与∠6是内错角,是直线AD和BC被AC所截形成的;∠ADC和∠DAB是同旁内角,是直线DC和AB被AD所截形成的
【解析】
(1)根据内错角就是:两个角都在截线的两侧,又分别处在被截的两条直线中间位置的位置的角,可得答案;
(2)根据同位角就是:两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角,可得答案;
(3)根据同旁内角就是:两个角都在截线的同旁,又分别处在被截的两条直线中间的位置的角,根据内错角就是:两个角都在截线的两侧,又分别处在被截的两条直线中间位置的位置的角,根据同位角就是:两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角,可得答案.
(1) DC和AB被AC所截得的内错角是∠1和∠5;
(2) AD和BC被AE所截得的同位角是∠DAB和∠9;
(3)∠4和∠7是内错角,是直线DC和AB被DB所截形成的;
∠2与∠6是内错角,是直线AD和BC被AC所截形成的;
∠ADC和∠DAB是同旁内角,是直线DC和AB被AD所截形成的.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(1)先化简![]() ,再任意选一个你喜欢的数作为x的值代入求值.
,再任意选一个你喜欢的数作为x的值代入求值.
(2)先化简,再求值:![]() ,其中a2-a=0.
,其中a2-a=0.
(3)已知y=![]() -x+3.试说明不论x为任何有意义的值,y的值均不变.
-x+3.试说明不论x为任何有意义的值,y的值均不变.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(﹣3,2),(b,m),(c,m),则点E的坐标是( ) 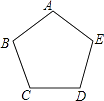
A.(2,﹣3)
B.(2,3)
C.(3,2)
D.(3,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
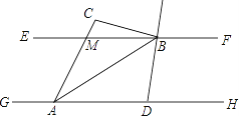
【题目】如图,已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB平分∠FBC,若∠ACB=100°,则∠DBA的度数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )

A. ∠A+∠C+∠D+∠E=360°
B. ∠A+∠D=∠C+∠E
C. ∠A-∠C+∠D+∠E=180°
D. ∠E-∠C+∠D-∠A=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
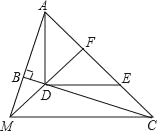
【题目】如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD、AB的延长线相交于点M,连接MC.
(1)求证:∠FMC=∠FCM;
(2)将条件中的AD⊥DE与(1)中的结论互换,其他条件不变,命题是否正确?请给出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日历上,我们可以发现其中某些数满足一定的规律.如图是2018年12月份的日历,我们任意选择其中所示的十字形部分,将每个部分中间数的左右两数,上下两数分别相乘,再把所得的结果相减.
(1)计算:11×13-5×19;16×18–10×24;(直接写结果)
(2)请你用整式的运算对以上的规律加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=10,AB=8,点E为边DC上一动点,连接AE,把△ADE沿AE折叠,使点D落在点D′处,当△DD′C是直角三角形时,DE的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求画图,并回答问题:
如图,在同一平面内有三点A,B,C.

(1)画直线AC;
(2)画射线CB;
(3)过点B作直线AC的垂线BD,垂足为D;
(4)画线段AB及线段AB的中点E,连接DE;
(5)通过画图和测量,与线段DE长度相等的线段有__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com