
【题目】如图,在平面直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 在第一象限内的图象相交于点
在第一象限内的图象相交于点![]() .
.
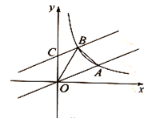
(1)求反比例函数的解析式;
(2)将直线![]() 向上平移后与反比例函数图象在第一象限内交于点
向上平移后与反比例函数图象在第一象限内交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的解析式.
的解析式.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)将A点坐标代入直线y=![]() x中求出m的值,确定出A的坐标,将A的坐标代入反比例解析式中求出k的值,即可确定出反比例函数的解析式;
x中求出m的值,确定出A的坐标,将A的坐标代入反比例解析式中求出k的值,即可确定出反比例函数的解析式;
(2)根据直线的平移规律设直线BC的解析式为y=![]() x+b,由同底等高的两三角形面积相等可得△ACO与△ABO面积相等,根据△ABO的面积为
x+b,由同底等高的两三角形面积相等可得△ACO与△ABO面积相等,根据△ABO的面积为![]() ,列出方程
,列出方程![]() OC2=
OC2=![]() ,解方程求出OC=
,解方程求出OC=![]() ,即b=
,即b=![]() ,进而得出直线BC的解析式.
,进而得出直线BC的解析式.
(1)(1)∵直线y=![]() x过点A(m,1),
x过点A(m,1),
∴![]() m=1,解得m=2,
m=1,解得m=2,
∴A(2,1).
∵反比例函数y=![]() (k≠0)的图象过点A(2,1),
(k≠0)的图象过点A(2,1),
∴k=2×1=2,
∴反比例函数的解析式为y=![]() ;
;
(2)连接AC,
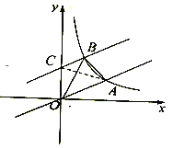
由平行线间的距离处处相等可得△ACO与△ABO面积相等,且△ABO的面积为![]() ,
,
∴△ACO的面积=![]() ,
,
∴![]()
∴直线![]() 的解析式
的解析式![]()


科目:初中数学 来源: 题型:
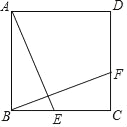
【题目】如图,正方形ABCD中,点E、F分别在边BC和DC上,连接AE、BF,AE⊥BF,点M、N分别在边AB、DC上,连接MN,若MN∥BC,FN=1,BE=2,则BM=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
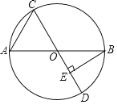
【题目】如图,AB为⊙O直径,点C是⊙O上一动点,过点C作⊙O直径CD,过点B作BE⊥CD于点E.已知AB=6cm,设弦AC的长为x cm,B,E两点间的距离为y cm(当点C与点A或点B重合时,y的值为0).
小冬根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小冬的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 0 | 0. 99 | 1. 89 | 2. 60 | 2. 98 | m | 0 |
经测量m的值为_____;(保留两位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图
象;

(3)结合画出的函数图象,解决问题:当BE=2时,AC的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
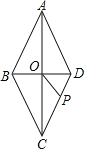
【题目】如图,在菱形ABCD中,两对角线AC、BD交于点O,AC=8,BD=6,当△OPD是以PD为底的等腰三角形时,CP的长为( )
A. 2B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
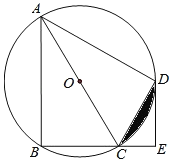
【题目】如图,四边形ABCD是⊙O的内接四边形,AC为直径,![]() ,DE⊥BC,垂足为E.
,DE⊥BC,垂足为E.
(1)判断直线ED与⊙O的位置关系,并说明理由;
(2)若CE=1,AC=4,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批单价为8元的商品,如果按每件10元出售,那么每天可销售100件,经调查发现,这种商品的销售单价每提高1元,其销售量相应减少10件.
(1)求销售量![]() 件与销售单价
件与销售单价![]() 元之间的关系式;
元之间的关系式;
(2)当销售单价![]() 定为多少,才能使每天所获销售利润最大?最大利润是多少?
定为多少,才能使每天所获销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加学校秋季运动会,有以下 5 个项目可供选择:径赛项目:100m、200m、1000m(分别用 A1、A2、A3 表示);田赛项目:跳远,跳高(分别用 T1、T2 表示).
(1)该同学从 5 个项目中任选一个,恰好是田赛项目的概率 P 为 ;
(2)该同学从 5 个项目中任选两个,求恰好是一个径赛项目和一个田赛项目的概率 P1,利用列表法或树状图加以说明;
(3)该同学从 5 个项目中任选两个,则两个项目都是径赛项目的概率 P2 为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
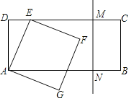
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() .点
.点![]() 从
从![]() 向
向![]() 以每秒
以每秒![]() 个单位的速度运动,以
个单位的速度运动,以![]() 为一边在
为一边在![]() 的右下方作正方形
的右下方作正方形![]() .同时垂直于
.同时垂直于![]() 的直线
的直线![]() 也从
也从![]() 向
向![]() 以每秒
以每秒![]() 个单位的速度运动,当经过________秒时.直线
个单位的速度运动,当经过________秒时.直线![]() 和正方形
和正方形![]() 开始有公共点?
开始有公共点?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com