
°æƒø°ø»ÁÕº£¨ABŒ™°—O÷±æ∂£¨µ„C «°—O…œ“ª∂ص„£¨π˝µ„C◊˜°—O÷±æ∂CD£¨π˝µ„B◊˜BE°ÕCD”⁄µ„E£Æ“—÷™AB=6cm£¨…Ëœ“ACµƒ≥§Œ™x cm£¨B£¨E¡Ωµ„º‰µƒæý¿ÎŒ™y cm(µ±µ„C”ε„AªÚµ„B÷ÿ∫œ ±£¨yµƒ÷µŒ™0)£Æ
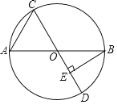
–°∂¨∏˘æð—ßœ∞∫Ø ˝µƒæ≠—È£¨∂‘∫Ø ˝yÀÊ◊‘±‰¡øxµƒ±‰ªØ∂¯±‰ªØµƒπʬ…Ω¯––¡ÀÃΩæø£Æ
œ¬√Ê «–°∂¨µƒÃΩæøπ˝≥㨫Î≤π≥‰ÕÍ’˚£∫
(1)Õ®π˝»°µ„°¢ª≠Õº°¢≤‚¡ø£¨µ√µΩ¡Àx”Îyµƒº∏◊È÷µ£¨»Áœ¬±Ì£∫
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 0 | 0. 99 | 1. 89 | 2. 60 | 2. 98 | m | 0 |
æ≠≤‚¡ømµƒ÷µŒ™_____£ª£®±£¡Ù¡ΩŒª–° ˝£©
(2)Ω®¡¢∆Ω√Ê÷±Ω«◊¯±Íœµ£¨√Ë≥ˆ“‘≤π»´∫Ûµƒ±Ì÷–∏˜∂‘∂‘”¶÷µŒ™◊¯±Íµƒµ„£¨ª≠≥ˆ∏√∫Ø ˝µƒÕº
œÛ£ª

£®3£©Ω·∫œª≠≥ˆµƒ∫Ø ˝ÕºœÛ£¨Ω‚戌 £∫µ±BE=2 ±£¨ACµƒ≥§∂»‘ºŒ™ cm.
 √˚ ¶µ„≤¶æÌœµ¡–¥∞∏
√˚ ¶µ„≤¶æÌœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨“‘BCŒ™÷±æ∂µƒ°—OΩªAC”⁄µ„E£¨π˝µ„E◊˜ABµƒ¥πœþΩªAB”⁄µ„F£¨ΩªCBµƒ—”≥§œþ”⁄µ„G£¨«“°œABG=2°œC£Æ
£®1£©«Û÷§£∫EG «°—Oµƒ«–œþ£ª
£®2£©»ÙtanC=![]() £¨AC=8£¨«Û°—Oµƒ∞Îæ∂£Æ
£¨AC=8£¨«Û°—Oµƒ∞Îæ∂£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ ±≥æ∞£∫‘⁄![]() ÷–£¨
÷–£¨![]() ±þ…œµƒ∂ص„
±þ…œµƒ∂ص„![]() ”…
”…![]() œÚ
œÚ![]() ‘À∂Ø£®”Î
‘À∂Ø£®”Î![]() £¨
£¨![]() ≤ª÷ÿ∫œ£©£¨µ„
≤ª÷ÿ∫œ£©£¨µ„![]() ”ε„
”ε„![]() Õ¨ ±≥ˆ∑¢£¨”…µ„
Õ¨ ±≥ˆ∑¢£¨”…µ„![]() —ÿ
—ÿ![]() µƒ—”≥§œþ∑ΩœÚ‘À∂Ø£®
µƒ—”≥§œþ∑ΩœÚ‘À∂Ø£®![]() ≤ª”Î
≤ª”Î![]() ÷ÿ∫œ£©£¨¡¨Ω·
÷ÿ∫œ£©£¨¡¨Ω·![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £¨µ„
£¨µ„![]() «œþ∂Œ
«œþ∂Œ![]() …œ“ªµ„.
…œ“ªµ„.
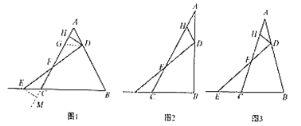
£®1£©≥ı≤Ω≥¢ ‘£∫»ÁÕº£¨»Ù![]() «µ»±þ»˝Ω«–Œ£¨
«µ»±þ»˝Ω«–Œ£¨![]() £¨«“µ„
£¨«“µ„![]() £¨
£¨![]() µƒ‘À∂ØÀŸ∂»œýµ»£¨«Û÷§£∫
µƒ‘À∂ØÀŸ∂»œýµ»£¨«Û÷§£∫![]() .
.
–°ÕıÕ¨—ß∑¢œ÷ø…“‘”…“‘œ¬¡Ω÷÷Àº¬∑Ω‚æˆ¥ÀŒ £∫
Àº¬∑“ª£∫π˝µ„![]() ◊˜
◊˜![]() £¨Ωª
£¨Ωª![]() ”⁄µ„
”⁄µ„![]() £¨œ»÷§
£¨œ»÷§![]() £¨‘Ÿ÷§
£¨‘Ÿ÷§![]() £¨¥”∂¯÷§µ√Ω·¬€≥…¡¢£ª
£¨¥”∂¯÷§µ√Ω·¬€≥…¡¢£ª
Àº¬∑∂˛£∫π˝µ„![]() ◊˜
◊˜![]() £¨Ωª
£¨Ωª![]() µƒ—”≥§œþ”⁄µ„
µƒ—”≥§œþ”⁄µ„![]() £¨œ»÷§
£¨œ»÷§![]() £¨‘Ÿ÷§
£¨‘Ÿ÷§![]() £¨¥”∂¯÷§µ√Ω·¬€≥…¡¢.
£¨¥”∂¯÷§µ√Ω·¬€≥…¡¢.
«Îƒ„»Œ—°“ª÷÷Àº¬∑£¨ÕÍ’˚µÿ È–¥±æ–°Ã‚µƒ÷§√˜π˝≥ã®»Á”√¡Ω÷÷∑Ω∑®◊˜¥£¨‘Ú“‘µ⁄“ª÷÷∑Ω∑®∆¿∑÷£©
£®2£©¿ý±»ÃΩæø£∫»ÁÕº£¨»Ù‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨«“µ„
£¨«“µ„![]() £¨
£¨![]() µƒ‘À∂ØÀŸ∂»÷Ʊ» «
µƒ‘À∂ØÀŸ∂»÷Ʊ» «![]() £¨«Û
£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®3£©—”…ÏÕÿ’π£∫»ÁÕº£¨»Ù‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨º«
£¨º«![]() £¨«“µ„
£¨«“µ„![]() °¢
°¢![]() µƒ‘À∂ØÀŸ∂»œýµ»£¨ ‘”√∫¨
µƒ‘À∂ØÀŸ∂»œýµ»£¨ ‘”√∫¨![]() µƒ¥˙ ˝ Ω±Ì æ
µƒ¥˙ ˝ Ω±Ì æ![]() £®÷±Ω”–¥≥ˆΩ·π˚£¨≤ª±ÿ–¥Ω‚¥π˝≥ã©.
£®÷±Ω”–¥≥ˆΩ·π˚£¨≤ª±ÿ–¥Ω‚¥π˝≥ã©.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄“ª∏ˆ∫Ï…´≤ªÕ∏√˜µƒ∫–◊”÷–∑≈”–Àƒ’≈∑÷±–¥”– ˝◊÷1£¨2£¨3£¨4µƒ∫Ï…´ø®∆¨£¨‘⁄“ª∏ˆ¿∂…´≤ªÕ∏√˜µƒ∫–◊”÷–∑≈”–»˝’≈∑÷±–¥”– ˝◊÷1£¨2£¨3µƒ¿∂…´ø®∆¨£¨ø®∆¨≥˝—’…´∫Õ ˝◊÷Õ‚ÕÍ»´œýÕ¨£Æ
£®1£©¥”∫Ï∫–÷–»Œ“‚≥È»°“ª’≈∫Ï…´ø®∆¨£¨¥”¿∂∫–÷–»Œ“‚≥È»°“ª’≈¿∂…´ø®∆¨£¨”√¡–æŸ∑®£® ˜–ŒÕºªÚ¡–±Ì∑®£©±Ì æÀ˘”–µƒø…ƒÐ«Èøˆ£ª
£®2£©«Û¡Ω’≈ø®∆¨…œ–¥”–œýÕ¨ ˝◊÷µƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
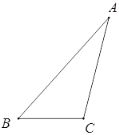
°æƒø°øœ¬√Ê «–°√˜…˺∆µƒ°∞◊˜»˝Ω«–Œµƒ∏þœþ°±µƒ≥þπÊ◊˜Õºπ˝≥Ã.
“—÷™£∫°˜ABC£Æ
«Û◊˜£∫BC±þ…œµƒ∏þœþ£Æ
◊˜∑®£∫»ÁÕº£¨
¢Ÿ“‘µ„CŒ™‘≤–ƒ£¨CAŒ™∞Îæ∂ª≠ª°£ª
¢⁄“‘µ„BŒ™‘≤–ƒ£¨BAŒ™∞Îæ∂ª≠ª°£¨¡Ωª°œýΩª”⁄µ„D£ª
¢€¡¨Ω”AD£¨ΩªBCµƒ—”≥§œþ”⁄µ„E£Æ
À˘“‘œþ∂ŒAEæÕ «À˘«Û◊˜µƒBC±þ…œµƒ∏þœþ£Æ
∏˘æð–°√˜…˺∆µƒ≥þπÊ◊˜Õºπ˝≥ã¨
£®1£© π”√÷±≥þ∫Õ‘≤πÊ£¨≤π»´Õº–Œ£ª£®±£¡Ù◊˜Õº∫€º££©
£®2£©ÕÍ≥…œ¬√Ê÷§√˜.
÷§√˜£∫°þCA=CD£¨
°ýµ„C‘⁄œþ∂ŒADµƒ¥π÷±∆Ω∑÷œþ…œ£® £© £®ÃÓÕ∆¿Ìµƒ“¿æ𣩣Æ
°þ = £¨
°ýµ„B‘⁄œþ∂ŒADµƒ¥π÷±∆Ω∑÷œþ…œ£Æ
°ý BC «œþ∂ŒADµƒ¥π÷±∆Ω∑÷œþ.
°ýAD°ÕBC£Æ
°ýAEæÕ «BC±þ…œµƒ∏þœþ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
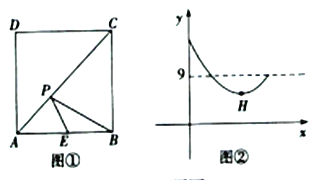
°æƒø°ø»ÁÕº¢Ÿ£¨‘⁄’˝∑Ω–Œ![]() ÷–£¨µ„
÷–£¨µ„![]() «
«![]() µƒ÷–µ„£¨µ„
µƒ÷–µ„£¨µ„![]() «∂‘Ω«œþ
«∂‘Ω«œþ![]() …œ“ª∂ص„£¨…Ë
…œ“ª∂ص„£¨…Ë![]() µƒ≥§∂»Œ™
µƒ≥§∂»Œ™![]() ”Î
”Î![]() µƒ≥§∂»∫ÕŒ™
µƒ≥§∂»∫ÕŒ™![]() £¨Õº¢⁄ «
£¨Õº¢⁄ «![]() πÿ”⁄
πÿ”⁄![]() µƒ∫Ø ˝ÕºœÛ£¨‘ÚÕºœÛ…œ◊ÓµÕµ„
µƒ∫Ø ˝ÕºœÛ£¨‘ÚÕºœÛ…œ◊ÓµÕµ„![]() µƒ◊¯±ÍŒ™_______.
µƒ◊¯±ÍŒ™_______.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕºÀ˘ 棨“—÷™≈◊ŒÔœþy=ax2+bx+c£®a°Ÿ0£©æ≠π˝µ„A£®©Å2£¨0£©°¢B£®4£¨0£©°¢C£®0£¨©Å8£©£¨”Î÷±œþy=x©Å4Ωª”⁄B£¨D¡Ωµ„
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω≤¢÷±Ω”–¥≥ˆDµ„µƒ◊¯±Í£ª
£®2£©µ„PŒ™÷±œþBDœ¬∑Ω≈◊ŒÔœþ…œµƒ“ª∏ˆ∂ص„£¨ ‘«Û≥ˆ°˜BDP√ʪ˝µƒ◊Ó¥Û÷µº∞¥À ±µ„Pµƒ◊¯±Í£ª
£®3£©µ„Q «œþ∂ŒBD…œ“Ï”⁄B°¢Dµƒ∂ص„£¨π˝µ„Q◊˜QF°Õx÷·”⁄µ„F£¨Ωª≈◊ŒÔœþ”⁄µ„G£¨µ±°˜QDGŒ™÷±Ω«»˝Ω«–Œ ±£¨÷±Ω”–¥≥ˆµ„Qµƒ◊¯±Í£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨÷±œþ![]() ”Î∑¥±»¿˝∫Ø ˝
”Î∑¥±»¿˝∫Ø ˝![]() ‘⁄µ⁄“ªœÛœÞƒ⁄µƒÕºœÛœýΩª”⁄µ„
‘⁄µ⁄“ªœÛœÞƒ⁄µƒÕºœÛœýΩª”⁄µ„![]() .
.
£®1£©«Û∑¥±»¿˝∫Ø ˝µƒΩ‚Œˆ Ω£ª
£®2£©Ω´÷±œþ![]() œÚ…œ∆Ω“∆∫Û”Î∑¥±»¿˝∫Ø ˝ÕºœÛ‘⁄µ⁄“ªœÛœÞƒ⁄Ωª”⁄µ„
œÚ…œ∆Ω“∆∫Û”Î∑¥±»¿˝∫Ø ˝ÕºœÛ‘⁄µ⁄“ªœÛœÞƒ⁄Ωª”⁄µ„![]() £¨”Î
£¨”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨«“
£¨«“![]() µƒ√ʪ˝Œ™
µƒ√ʪ˝Œ™![]() £¨«Û÷±œþ
£¨«Û÷±œþ![]() µƒΩ‚Œˆ Ω.
µƒΩ‚Œˆ Ω.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨∂˛¥Œ∫Ø ˝![]() Ωª
Ωª![]() ÷·”⁄
÷·”⁄![]() °¢
°¢![]() ¡Ωµ„£¨£®µ„
¡Ωµ„£¨£®µ„![]() ‘⁄µ„
‘⁄µ„![]() µƒ◊Û≤ý£©”Î
µƒ◊Û≤ý£©”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £Æ
£Æ
£®1£©«Ûµ„![]() °¢µ„
°¢µ„![]() ∫Õµ„
∫Õµ„![]() µƒ◊¯±Í£ª
µƒ◊¯±Í£ª
£®2£©»ÁÕº2£¨»Ùµ„![]() Œ™µ⁄ÀƒœÛœÞƒ⁄≈◊ŒÔœþ…œ“ª∂ص„£¨µ„
Œ™µ⁄ÀƒœÛœÞƒ⁄≈◊ŒÔœþ…œ“ª∂ص„£¨µ„![]() µƒ∫·◊¯±ÍŒ™
µƒ∫·◊¯±ÍŒ™![]() £¨
£¨![]() µƒ√ʪ˝Œ™
µƒ√ʪ˝Œ™![]() £Æ«Û
£Æ«Û![]() πÿ”⁄
πÿ”⁄![]() µƒ∫Ø ˝πÿœµ Ω£¨≤¢«Û≥ˆ
µƒ∫Ø ˝πÿœµ Ω£¨≤¢«Û≥ˆ![]() µƒ◊Ó¥Û÷µ£ª
µƒ◊Ó¥Û÷µ£ª
£®3£©≈◊ŒÔœþµƒ∂‘≥∆÷·…œ «∑ҥʑ⁄µ„![]() £¨ π
£¨ π![]() Œ™µ»—¸»˝Ω«–Œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆÀ˘”–µ„
Œ™µ»—¸»˝Ω«–Œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆÀ˘”–µ„![]() µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com