
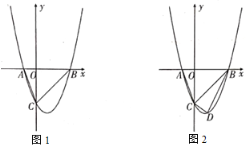
【题目】如图1,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,(点
两点,(点![]() 在点
在点![]() 的左侧)与
的左侧)与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)求点![]() 、点
、点![]() 和点
和点![]() 的坐标;
的坐标;
(2)如图2,若点![]() 为第四象限内抛物线上一动点,点
为第四象限内抛物线上一动点,点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() .求
.求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值;
的最大值;
(3)抛物线的对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出所有点
为等腰三角形?若存在,请直接写出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
科目:初中数学 来源: 题型:
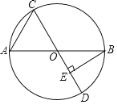
【题目】如图,AB为⊙O直径,点C是⊙O上一动点,过点C作⊙O直径CD,过点B作BE⊥CD于点E.已知AB=6cm,设弦AC的长为x cm,B,E两点间的距离为y cm(当点C与点A或点B重合时,y的值为0).
小冬根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小冬的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 0 | 0. 99 | 1. 89 | 2. 60 | 2. 98 | m | 0 |
经测量m的值为_____;(保留两位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图
象;

(3)结合画出的函数图象,解决问题:当BE=2时,AC的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加学校秋季运动会,有以下 5 个项目可供选择:径赛项目:100m、200m、1000m(分别用 A1、A2、A3 表示);田赛项目:跳远,跳高(分别用 T1、T2 表示).
(1)该同学从 5 个项目中任选一个,恰好是田赛项目的概率 P 为 ;
(2)该同学从 5 个项目中任选两个,求恰好是一个径赛项目和一个田赛项目的概率 P1,利用列表法或树状图加以说明;
(3)该同学从 5 个项目中任选两个,则两个项目都是径赛项目的概率 P2 为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
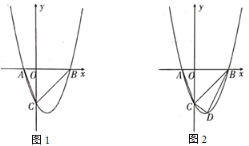
【题目】如图1,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,(点
两点,(点![]() 在点
在点![]() 的左侧)与
的左侧)与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)求点![]() 、点
、点![]() 和点
和点![]() 的坐标;
的坐标;
(2)如图2,若点![]() 为第四象限内抛物线上一动点,点
为第四象限内抛物线上一动点,点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() .求
.求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值;
的最大值;
(3)抛物线的对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出所有点
为等腰三角形?若存在,请直接写出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为![]() ,看这栋大楼底部C的俯角为
,看这栋大楼底部C的俯角为![]() ,热气球A的高度为270米,则这栋大楼的高度为______米
,热气球A的高度为270米,则这栋大楼的高度为______米![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面说法正确的是个数有( )
①如果三角形三个内角的比是1:2:3,那么这个三角形是直角三角形;
②如果三角形的一个外角等于与它相邻的一个内角,则这么三角形是直角三角形;
③如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是直角三角形;
④如果∠A=∠B=![]() ∠C,那么△ABC是直角三角形;
∠C,那么△ABC是直角三角形;
⑤若三角形的一个内角等于另两个内角之差,那么这个三角形是直角三角形;
⑥在△ABC中,若∠A+∠B=∠C,则此三角形是直角三角形.
A.3个 B.4个 C.5个 D.6个
查看答案和解析>>
科目:初中数学 来源: 题型:
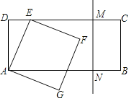
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() .点
.点![]() 从
从![]() 向
向![]() 以每秒
以每秒![]() 个单位的速度运动,以
个单位的速度运动,以![]() 为一边在
为一边在![]() 的右下方作正方形
的右下方作正方形![]() .同时垂直于
.同时垂直于![]() 的直线
的直线![]() 也从
也从![]() 向
向![]() 以每秒
以每秒![]() 个单位的速度运动,当经过________秒时.直线
个单位的速度运动,当经过________秒时.直线![]() 和正方形
和正方形![]() 开始有公共点?
开始有公共点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学们的课余生活,我校将在周末举行“亲近大自然”的社会实践活动,现随机抽取了部分学生进行主题为“你最想去的景点是千鹤湖公园”的问卷调查,要求学生只能从“A(华中工委纪念馆),B(洋马菊花园),C(千鹤湖公园),D(丹顶鹤自然保护区)”四个景点中选择一项,根据调查结果,绘制了如图的两幅不完整的统计图:
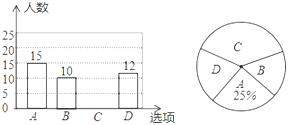
请解答下列问题:
(1)本次调查的样本容量是 ;
(2)补全条形统计图;
(3)在扇形统计图中,求B所占的圆心角度数;
(4)若该校有3600名学生,试估计该校最想去千鹤湖公园的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com