
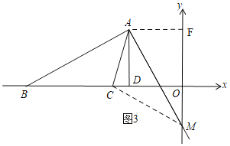
【题目】在平面直角坐标系中,点A的坐标为(﹣6,6),以A为顶点的∠BAC的两边始终与x轴交于B、C两点(B在C左面),且∠BAC=45°.
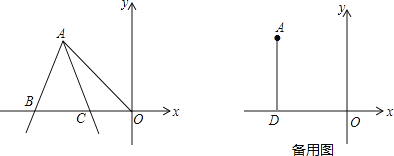
(1)如图,连接OA,当AB=AC时,试说明:OA=OB.
(2)过点A作AD⊥x轴,垂足为D,当DC=2时,将∠BAC沿AC所在直线翻折,翻折后边AB交y轴于点M,求点M的坐标.
【答案】(1)见解析;(2) M的坐标为(0,3)或(0,-6)
【解析】
(1)利用等腰三角形的性质求得∠BAO和∠ABC的度数,然后利用等角对等边即可证得;
(2)当点C在点D右侧时,连接CM,过点A作AE⊥y轴于点E,证明△BAD≌△MAE,在Rt△COM中,由勾股定理即可求得M的坐标;当点C在点D左侧时,连接CM,过点A作AF⊥y轴于点F,证明△BAD≌△MAF,同理,在Rt△COM中,由勾股定理即可求得M的坐标.
(1)∵AB=AC,∠BAC=45°,
∴∠ABC=∠ACB=67.5°.
过点A作AE⊥OB于E,
∵A(-6,6),
∴△AEO是等腰直角三角形,∠EAO=45°.
∵AB=AC,AE⊥OB,
∴∠BAE=![]() ∠BAC=22.5°.
∠BAC=22.5°.
∴∠BAO=67.5°=∠ABC,
∴OA=OB.
(2)设OM=x,
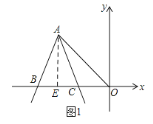
当点C在点D右侧时,如图2,连接CM,过点A作AE⊥y轴于点E,
由∠BAM=∠DAE=90°,
可知:∠BAD=∠MAE;
∴在△BAD和△MAE中,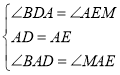 ,
,
∴△BAD≌△MAE.
∴BD=EM=6-x.
又∵AC=AC,∠BAC=∠MAC,
∴△BAC≌△MAC.
∴BC=CM=8-x.
在Rt△COM中,由勾股定理得:
OC2+OM2=CM2,即42+x2=(8-x)2,
解得:x=3,
∴M点坐标为(0,3).
当点C在点D左侧时,如图3,连接CM,过点A作AF⊥y轴于点F,
同理,△BAD≌△MAF,
∴BD=FM=6+x.
同理,
△BAC≌△MAC,
∴BC=CM=4+x.
在Rt△COM中,由勾股定理得:
OC2+OM2=CM2,即82+x2=(4+x)2,
解得:x=6,
∴M点坐标为(0,-6).
综上,M的坐标为(0,3)或(0,-6).


科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD,点 E,F 分别在 AD,CD 上,且DE=CF,AF 与 BE 相交于点G.
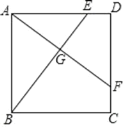
(1)求证:AF⊥BE;
(2)若 AB=6,DE=2,AG的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,以
,以![]() 边
边![]() 和
和![]() 为边作等边
为边作等边![]() 和
和![]() ,连接
,连接![]() ,
,![]() ,
,
![]() 判断
判断![]() 与
与![]() 的数量关系,并求
的数量关系,并求![]() 与
与![]() 的夹角
的夹角![]() 的度数;
的度数;
![]() 继续探索,如图
继续探索,如图![]() ,以
,以![]() 的
的![]() 和
和![]() 为边作正方形
为边作正方形![]() 和
和![]() ,连接
,连接![]() 、
、![]() ,判断
,判断![]() 和
和![]() 的数量关系,并求出此时
的数量关系,并求出此时![]() 与
与![]() 的夹角;
的夹角;
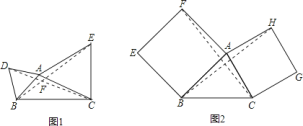
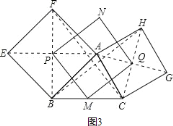
![]() 如图
如图![]() 中
中![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 分别是正方形的中心,顺次连接
分别是正方形的中心,顺次连接![]() ,判断四边形
,判断四边形![]() 的形状并证明.
的形状并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数![]() 的图象与性质,下列结论错误的是 ( )
的图象与性质,下列结论错误的是 ( )
A. 当x=3时,函数有最大值-2
B. 当x>3时,y随x的增大而减小
C. 抛物线可由 ![]() 经过平移得到
经过平移得到
D. 该函数的图象与x轴有两个交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.(售价不低于进价).请根据小丽提供的信息,解答小华和小明提出的问题.

认真阅读上面三位同学的对话,请根据小丽提供的信息.
(1)解答小华的问题;
(2)解答小明的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=-1,与x轴的一个交点为(x1,0),且0<x1<1,下列结论:①9a-3b+c>0;②b<c;③3a+c>0,其中正确结论两个数有______。
查看答案和解析>>
科目:初中数学 来源: 题型:
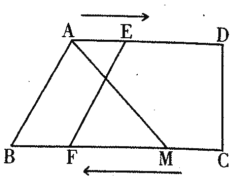
【题目】如图,四边形ABCD中,AD∥BC,AD=8cm,BC=12cm,M是BC上一点,且BM=9cm,点E从点A出发以1cm/s的速度向点D运动,点F从点C出发,以3cm/s的速度向点B运动,当其中一点到达终点,另一点也随之停止,设运动时间为t,则当以A、M、E、F为顶点的四边形是平行四边形时,t=__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com