
��ͼ������ABCD����AB��CD��AB=14��AD= 4 ��CD=7��ֱ��l����A��D���㣬��sin��DAB=
��CD=7��ֱ��l����A��D���㣬��sin��DAB= ������P���߶�AB�ϴӵ�A������ÿ��2����λ���ٶ����B�˶���ͬʱ����Q�ӵ�B������ÿ��5����λ���ٶ���B��C��D�ķ������D�˶�������P��PM��ֱ��AB��������A��D��C�ཻ�ڵ�M����P��Q��������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������P��Q�˶���ʱ��Ϊt�루t��0������MPQ�����ΪS��
������P���߶�AB�ϴӵ�A������ÿ��2����λ���ٶ����B�˶���ͬʱ����Q�ӵ�B������ÿ��5����λ���ٶ���B��C��D�ķ������D�˶�������P��PM��ֱ��AB��������A��D��C�ཻ�ڵ�M����P��Q��������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������P��Q�˶���ʱ��Ϊt�루t��0������MPQ�����ΪS��

��1������BC�ij���
��2����Q��BC���˶�ʱ����S��t�ĺ�����ϵʽ��
��3���ڣ�2���������£��Ƿ����ijһʱ��t��ʹ����MPQ�����S������ABCD����� �������ڣ������t��ֵ��������������˵��������
�������ڣ������t��ֵ��������������˵��������
��4������P��Q������˶�������M���߶�DC���˶�ʱ����PM���ӳ�����ֱ��l�ཻ�ڵ�N����̽������tΪ��ֵʱ����QMNΪ���������Σ�
��1��5����2��S=��5t2+14t(0��t��1����3�������ڣ����ɼ���������4��t=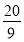 ��t=
��t=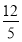
��������
�����������1��������������ȷ����D�����꣬����sin��DAB= �������Ǻ���ֵ���õ���AODΪ����ֱ�������Σ�������εĸߣ�Ȼ�����ù��ɶ������BC�г���
�������Ǻ���ֵ���õ���AODΪ����ֱ�������Σ�������εĸߣ�Ȼ�����ù��ɶ������BC�г���
��2����0��t��1ʱ��S= ��2t����14��5t��=��5t2+14t��
��2t����14��5t��=��5t2+14t��
��3���ڣ�2���������£�������ijһʱ��t��ʹ�á�MPQ�����S������ABCD�����
��4����QMNΪ���������ε����������֣���Ҫ�������ۣ�����©�⣮
�����������1��5
��2����0��t��1ʱ��S= ��2t����14��5t��=��5t2+14t
��2t����14��5t��=��5t2+14t
��3������ABCD�����Ϊ42
��5t2+14t=
 42���⣬���ԡ�MPQ���������Ϊ����ABCD��
42���⣬���ԡ�MPQ���������Ϊ����ABCD�� ��
��
��4����QMN��������������������
����ͼ4��ʾ����M���߶�NM���Ҳ���
 ��
��
MQ=CD-DM-CQ=7-��2t-4��-��5t-5��=16-7t��MN=DM=2t-4��
��MN=MQ����16-7t=2t-4�����t=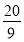 ��
��
����ͼ5��ʾ����Q��MN�����ʱ��5t-5+��2t-4��-7=��2t-4��+4-4��

��ã�t=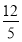 ��
��
�ʵ�t=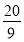 ��t=
��t=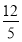 ʱ����QMNΪ���������Σ�
ʱ����QMNΪ���������Σ�
����: һ�κ����ۺ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2013-2014ѧ��㶫ʡ�Ƹ��о��꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
ij�����û�������ij�ֻ��磬����ʵ�鷢��ÿ���ӯ����ÿ�����������һ���Ĺ�ϵ��ÿ��ֲ��3��ʱ��ƽ������ӯ��3Ԫ����ͬ����������������ÿ������1�꣬ƽ������ӯ���ͼ���0��5Ԫ��Ҫʹÿ���ӯ���ﵽ10Ԫ��ÿ��Ӧ��ֲ�����ꣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ��㶫ʡ�п�Ԥ�����ѧ�Ծ��������棩 ���ͣ�ѡ����
���м�����ȷ���ǣ�������
A��a3•a4=a12 B����a3��4=a7
C����a2b��3=a6b3 D��a3��a4=a��a��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ��㶫��ͷ�о��꼶��ѧ�ڵ�һ�νο�����ѧ�Ծ��������棩 ���ͣ������
������ �Ķ��������� .
�Ķ��������� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ��㶫��ͷ�о��꼶��ѧ�ڵ�һ�νο�����ѧ�Ծ��������棩 ���ͣ�ѡ����
���м����������ǣ� ����
A�� B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ��ɽ���ൺƽ�ȹ��������ѧ���꼶��ѧ�ڽ������������ѧ�Ծ��������棩 ���ͣ������
��ҹ�Ʒ���������г�����ij��ˮ�����ۣ���һ����1200Ԫ��������ǧ�ˣ�����ÿǧ��8Ԫ���ۣ��ܿ����꣮����ˮ���������ڶ��ι���ʱ��ÿǧ�˵Ľ��۱ȵ�һ�������10%����1452Ԫ������������ȵ�һ�ζ�20ǧ �ˣ���ÿǧ��9Ԫ�۳�100ǧ�˺�����ָ���������ˮ�����ױ��ʣ�Ϊ������ʧ���㽵��50%����ʣ���ˮ����
��1�����һ��ˮ���Ľ�����ÿǧ�˶���Ԫ��
��2���ù�Ʒ���������������У���������ӯ�� ���ǿ���ӯ��������˶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ��ɽ���ൺƽ�ȹ��������ѧ���꼶��ѧ�ڽ������������ѧ�Ծ��������棩 ���ͣ������
��ͼ��ֱ�� ��x�ᡢy ��ֱ��ڵ�A �͵�B ����C��ֱ��AB�ϣ��ҵ�C ��������Ϊ��1 ����D �ڷ���������
��x�ᡢy ��ֱ��ڵ�A �͵�B ����C��ֱ��AB�ϣ��ҵ�C ��������Ϊ��1 ����D �ڷ��������� ��ͼ���� ��CDƽ����y�ᣬ
��ͼ���� ��CDƽ����y�ᣬ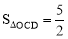 ����k��ֵΪ ��
����k��ֵΪ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ��ɽ��ʡ����ѧҵˮƽ������ѧģ���Ծ��������棩 ���ͣ������
��������������С����,��ѡ��һ��ɼ��ɣ�
(1)������ʽ�� �������⣮
�������⣮
(2)���㣺
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ��ɽ��ʡ�Ͳ��л�̨�ؾ��꼶�п�ģ����ѧ�Ծ��������棩 ���ͣ�ѡ����
���б�����ȷ���ǣ�������
A��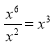 B��
B��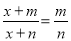 C��
C�� D��
D��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com