
【题目】判断以下各题的结论是否正确(对的打“√”,错的打“×”).
(1)若 b﹣3a<0,则b<3a;
(2)如果﹣5x>20,那么x>﹣4;
(3)若a>b,则 ac2>bc2;
(4)若ac2>bc2 , 则a>b;
(5)若a>b,则 a(c2+1)>b(c2+1).
(6)若a>b>0,则![]() <
<![]() .
.
【答案】解:(1)若由b﹣3a<0,移项即可得到b<3a,故正确;
(2)如果﹣5x>20,两边同除以﹣5不等号方向改变,故错误;
(3)若a>b,当c=0时则 ac2>bc2错误,故错误;
(4)由ac2>bc2得c2>0,故正确;
(5)若a>b,根据c2+1,则 a(c2+1)>b(c2+1)正确.
(6)若a>b>0,如a=2,b=1,则![]() <
<![]() . 正确.
. 正确.
故答案为:√、×、×、√、√、√.
【解析】利用不等式的性质逐个判断即可.
【考点精析】利用不等式的性质对题目进行判断即可得到答案,需要熟知1:不等式的两边同时加上(或减去)同一个数(或式子),不等号的方向不变 .2:不等式的两边同时乘以(或除以)同一个 正数 ,不等号的方向 不变 .3:不等式的两边同时乘以(或除以)同一个 负数 ,的方向 改变.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.
求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列单项式按以下规律排列:a,3a2 , 5a3 , 7a,9a2 , 11a3 , 13a,…,则第2016个单项式应是( )
A.4031a3
B.4031a
C.4031a2
D.4032a3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要使多项式(x2+px+2)(x﹣q)不含关于x的二次项,则p与q的关系是( )
A. 相等 B. 互为相反数 C. 互为倒数 D. 乘积为﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2 , 也可以表示为4×![]() ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 .
ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 . 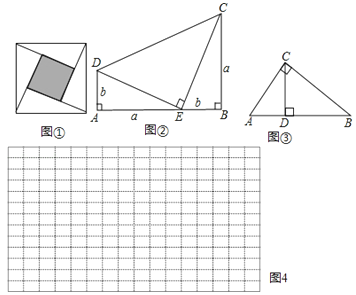
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,直角△ABC中,∠ACB=90°,AC=3cm,BC=4cm,则斜边AB上的高CD的长为.
(3)试构造一个图形,使它的面积能够解释(a+b)(a+2b)=a2+3ab+2b2 , 画在如图4的网格中,并标出字母a、b所表示的线段.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com