
����Ŀ�����Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ�
��1����ͼ1���ı���ABCD�У���E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣮
��֤���е��ı���EFGH��ƽ���ı��Σ�
��2����ͼ2����P���ı���ABCD��һ�㣬������PA=PB��PC=PD����APB=��CPD����E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣬�����е��ı���EFGH����״����֤����IJ��룻
��3�����ı䣨2���е�������ʹ��APB=��CPD=90�㣬�����������䣬ֱ��д���е��ı���EFGH����״��������֤����
���𰸡�
��1��
֤������ͼ1�У�����BD��
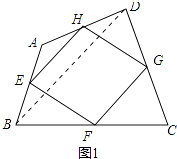
�ߵ�E��H�ֱ�Ϊ��AB��DA���е㣬
��EH��BD��EH= ![]() BD��
BD��
�ߵ�F��G�ֱ�Ϊ��BC��CD���е㣬
��FG��BD��FG= ![]() BD��
BD��
��EH��FG��EH=GF��
���е��ı���EFGH��ƽ���ı��Σ�
��2��
�ı���EFGH�����Σ�
֤������ͼ2�У�����AC��BD��
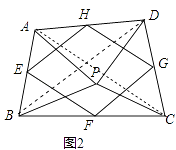
�ߡ�APB=��CPD��
���APB+��APD=��CPD+��APD
����APC=��BPD��
�ڡ�APC�͡�BPD�У�
 ��
��
���APC�ա�BPD��
��AC=BD
�ߵ�E��F��G�ֱ�Ϊ��AB��BC��CD���е㣬
��EF= ![]() AC��FG=
AC��FG= ![]() BD��
BD��
���ı���EFGH��ƽ���ı��Σ�
���ı���EFGH�����Σ�
��3��
�ı���EFGH�������Σ�
֤������ͼ2�У�

��AC��BD���ڵ�O��AC��PD���ڵ�M��AC��EH���ڵ�N��
�ߡ�APC�ա�BPD��
���ACP=��BDP��
�ߡ�DMO=��CMP��
���COD=��CPD=90�㣬
��EH��BD��AC��HG��
���EHG=��ENO=��BOC=��DOC=90�㣬
���ı���EFGH�����Σ�
���ı���EFGH�������Σ�
����������1����ͼ1�У�����BD��������������λ�߶���ֻҪ֤��EH��FG��EH=FG���ɣ���2���ı���EFGH�����Σ���֤����APC�ա�BPD���õ�AC=BD����֤��EF=FG���ɣ���3���ı���EFGH�������Σ�ֻҪ֤����EHG=90�㣬���á�APC�ա�BPD���á�ACP=��BDP������֤����COD=��CPD=90�㣬�ٸ���ƽ���ߵ����ʼ���֤����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
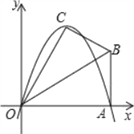
����Ŀ����֪��Rt��OAB��,��OAB=90��,��BOA=30��,AB=2.����OΪ����ԭ��,OA����ֱ��Ϊx�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵ,��B�ڵ�һ������.��Rt��OAB��OB�۵���,��A���ڵ�һ�����ڵĵ�C����
��1�����C�����ꣻ
��2����������y=ax2+bx��a��0������C��A���㣬��������ߵĽ���ʽ��
��3���������ߵĶԳ�����OB���ڵ�D,��PΪ�߶�DB��һ��,��P��y���ƽ����,���������ڵ�M����:�Ƿ���������ĵ�P,ʹ���ı���CDPMΪ�������Σ�������,�������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABC��DE�۵���ʹ��A����BC�ϵĵ�F������DE��BC������B��70�����BDF�� �� 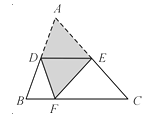
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AD��BE�Ǹߣ���ABE=45������F��AB���е㣬AD��FE��BE�ֱ��ڵ�G��H����CBE=��BAD�������н��ۣ���FD=FE����AH=2CD����BCAD=![]() AE2���ܡ�DFE=2��DAC ;��������CH����CH��EF.������ȷ�ĸ���Ϊ�� ��
AE2���ܡ�DFE=2��DAC ;��������CH����CH��EF.������ȷ�ĸ���Ϊ�� ��
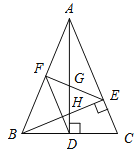
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ��������ij�Ϊ2a �� ��Ҳ��2a �� ��Ϊh.
��1����a ��h�Ĵ���ʽ��ʾ�ó���������������. ![]()
��2����a=3��h= ![]() ʱ������Ӧ����������������.
ʱ������Ӧ����������������.
��3����(2)�Ļ����ϣ��ѳ�����x �� ������x �� ����0��x��6���ʳ����������Ƿ����仯����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ѷ���x��5x��4��+1=2��Ϊһ����ʽ�����������ϵ��Ϊ5����һ����ϵ��Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�Ƕ�ԲO���ڽ������Σ�ADΪ��ABC�ĸ��ߣ�AEƽ����BAC����O��E����BC��G����OE��BC��F����OA�������н����У� ��CE��2EF���ڡ�ABG�ס�AEC���ۡ�BAO����DAC����![]() Ϊ������������ȷ����______��
Ϊ������������ȷ����______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ж����¸���Ľ����Ƿ���ȷ���ԵĴ̡������Ĵ�������
��1���� b��3a��0����b��3a����
��2�������5x��20����ôx����4����
��3����a��b���� ac2��bc2����
��4����ac2��bc2 �� ��a��b����
��5����a��b���� a��c2+1����b��c2+1����
��6����a��b��0����![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com