练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知一个等腰三角形两内角的度数之比为1：4，则这个等腰三角形顶角的度数为 ．

    【答案】120°或20°
    【解析】解：设两个角分别是x，4x ①当x是底角时，根据三角形的内角和定理，得x+x+4x=180°，解得，x=30°，4x=120°，即底角为30°，顶角为120°；
    ②当x是顶角时，则x+4x+4x=180°，解得，x=20°，从而得到顶角为20°，底角为80°；
    所以该三角形的顶角为120°或20°．
    故答案为：120°或20°．
    设两个角分别是x，4x，根据三角形的内角和定理分情况进行分析，从而可求得顶角的度数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知y＝（a﹣1）x+2a﹣4，当x＝﹣1时，y＝0．

    （1）求a的值；

    （2）当x＝1时，求y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

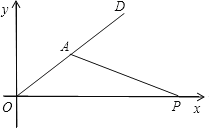
    【题目】随着科学技术的发展，机器人早已能按照设计的指令完成各种动作．在坐标平面上，根据指令[S，α]（S≥0，0°＜α＜180°）机器人能完成下列动作：先原地顺时针旋转角度α，再朝其对面方向沿直线行走距离s．

    （1）填空：如图，若机器人在直角坐标系的原点，且面对y轴的正方向，现要使其移动到点A（2，2），则给机器人发出的指令应是 ；

    （2）机器人在完成上述指令后，发现在P（6，0）处有一小球正向坐标原点做匀速直线运动，已知小球滚动的速度与机器人行走的速度相同，若忽略机器人原地旋转的时间，请你给机器人发一个指令，使它能截住小球．

    （参考数据：sin53°≈0.8，cos37°≈0.80，tan37°≈0.75，tan26.5°≈0.5）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，经过圆上点D的直线CD恰使∠ADC=∠B．

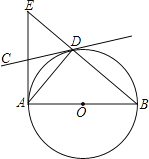
    （1）求证：直线CD是⊙O的切线；

    （2）过点A作直线AB的垂线交BD的延长线于点E，且AB=5，BD=2，求线段AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知等腰三角形的两边长分别为7和3，则第三边的长是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两个口袋中均有三张除所标数值外完全相同的卡片，甲袋中的三张卡片上所标的数值分别为﹣7，﹣1，3，乙袋中的三张卡片上所标的数值分别为﹣2，1，6．先从甲袋中随机取出一张卡片，用x表示取出的卡片上标的数值，再从乙袋中随机取出一张卡片，用y表示取出的卡片上标的数值，把x，y分别作为点A的横坐标和纵坐标．

    （1）请用列表或画树状图法，表示出点A（x，y）所有可能出现的结果；

    （2）求点A在第三象限的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果一个三角形三条边的长分别是7，24，25，则这个三角形的最大内角的度数是（　　）

    A.30°B.45°C.60°D.90°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

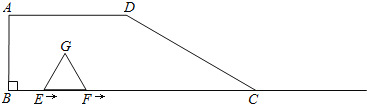
    【题目】如图，在梯形ABCD中，AD∥BC，∠B=90°，BC=6，AD=3，∠DCB=30°．点E、F同时从B点出发，沿射线BC向右匀速移动，已知F点移动速度是E点移动速度的2倍，以EF为一边在CB的上方作等边△EFG，设E点移动距离为x（x＞0）．

    （1）△EFG的边长是 （用含有x的代数式表示），当x=2时，点G的位置在 ；

    （2）若△EFG与梯形ABCD重叠部分面积是y，求y与x之间的函数关系式；

    （3）探究（2）中得到的函数y在x取何值时，存在最大值？并求出最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】判定两个直角三角形全等的方法有 ．

    查看答案和解析>>

    同步练习册答案