
����Ŀ���ھ���ƶ�Ĺ����У�ijפ�����ӽ�ϵ��ظ�ɽ���Σ������ڸô���ֲ��ҩ�Ĵ��㡢��ĸ���������Ӿ������ˣ�����һ��ʱ�䣬�ô�����ֲ�Ĵ��㡢��ĸ���������֮��4:3:5���Ǹ�����ҩ���г��Դ��㡢��ĸ�������������������ڸô����������ϼ�����ֲ��������ҩ�ģ��������轫�������������![]() ��ֲ�������������ֲ��������ﵽ��������ҩ����ֲ�������
��ֲ�������������ֲ��������ﵽ��������ҩ����ֲ�������![]() ��Ϊʹ������ֲ������뱴ĸ��ֲ�����֮�ȴﵽ3:4����ô廹����ֲ��ĸ�������ô���ֲ��������ҩ�ĵ������֮����____��
��Ϊʹ������ֲ������뱴ĸ��ֲ�����֮�ȴﵽ3:4����ô廹����ֲ��ĸ�������ô���ֲ��������ҩ�ĵ������֮����____��
���𰸡�3:20
��������
��ô�����ҩ�����x�������������Ϊy��������ֲ��ĸ�����Ϊz���������Ϊ��x+y������������ֲ���![]() x����ĸ����ֲ���
x����ĸ����ֲ���![]() x����������ֲ���
x����������ֲ���![]() x���������г������飬��y�Ĵ���ʽ�ֱ��ʾx��y��Ȼ����м��㼴��.
x���������г������飬��y�Ĵ���ʽ�ֱ��ʾx��y��Ȼ����м��㼴��.
�⣺��ô�����ҩ�����x�������������Ϊy��������ֲ��ĸ�����Ϊz���������Ϊ��x+y������������ֲ���![]() x����ĸ����ֲ���
x����ĸ����ֲ���![]() x����������ֲ���
x����������ֲ���![]() x
x
������ɵã�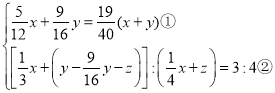
������![]()
������������![]()
�ĸ�������ô���ֲ��������ҩ�ĵ������֮��=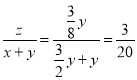
�ʴ�Ϊ3��20.


 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
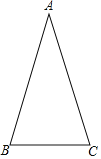
����Ŀ�� ��ͼ���ڡ�ABC�У�AB��AC��
��1���ó߹���ͼ����AC������һ��D��ʹ��BD��BC��������ͼ�ۼ�����Ҫ��д��������
��2������A��30�㣬���ABD�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ��
��![]() ��
��![]() �ߵ��е㣬��
�ߵ��е㣬��![]() ����������һ���㣬
����������һ���㣬![]() ������
������![]() �����߶�
�����߶�![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ��
��![]() ������
������![]() ��
��![]() �����߶�
�����߶�![]() ������Сֵ�� ��
������Сֵ�� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ó��˾����ij��ˮ���ijɱ�Ϊ20Ԫ/kg�������г����з��֣�����ˮ����δ��48������۵���p��Ԫ/kg����ʱ��t���죩֮��ĺ�����ϵʽΪ��
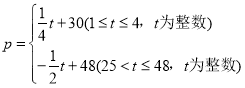 ��������������y��kg����ʱ��t���죩�Ĺ�ϵ���±���
��������������y��kg����ʱ��t���죩�Ĺ�ϵ���±���

��1����֪y��t֮��ı仯���ɷ���һ�κ�����ϵ�������ڵ�30������������Ƕ��٣�
��2������һ���������������������������Ϊ���٣�
��3����ʵ�����۵�ǰ24���У���˾����ÿ����1kgˮ���;���nԪ����n��9����������ƶ�������ַ��֣���ǰ24���У�ÿ��۳��������������������ʱ��t�������������n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
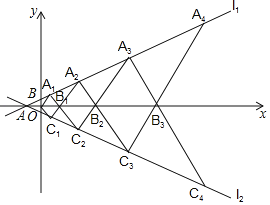
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l2��![]() ��x�ύ�ڵ�A����y�ύ�ڵ�B����x��Ϊ�Գ�����ֱ��
��x�ύ�ڵ�A����y�ύ�ڵ�B����x��Ϊ�Գ�����ֱ��![]() ����Գ�ͼ�ε�ֱ��l2����A1��A2��A3����ֱ��l1�ϣ���B1��B2��B3����x�������ϣ���C1��C2��C3����ֱ��l2�ϣ�����A1B1O����A2B2B1����A2B1B2������AnBnBn��1��Ϊ�ȱ������Σ��ı���A1B1C1O���ı���A2B2C2B1���ı���A2B1C2B2�����ı���AnBnnBn��1������ֱ���S1��S2��S3������Sn����SnΪ_____�����ú���n�Ĵ���ʽ��ʾ��
����Գ�ͼ�ε�ֱ��l2����A1��A2��A3����ֱ��l1�ϣ���B1��B2��B3����x�������ϣ���C1��C2��C3����ֱ��l2�ϣ�����A1B1O����A2B2B1����A2B1B2������AnBnBn��1��Ϊ�ȱ������Σ��ı���A1B1C1O���ı���A2B2C2B1���ı���A2B1C2B2�����ı���AnBnnBn��1������ֱ���S1��S2��S3������Sn����SnΪ_____�����ú���n�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ڽ�����ϵ�У�������y=x2-2x-3��x�ύ���A��B����A�ڵ�B����ࣩ��y���ڵ�C����DΪ�����ߵĶ��㣬�Գ�����x�ύ�ڵ�E��
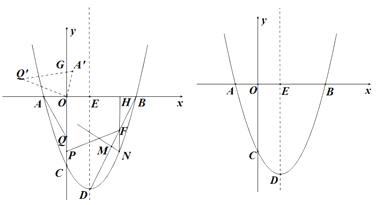
��1������BD����M���߶�BD��һ���㣨��M����˵�B��D�غϣ�������M��MN��BD���������ڵ�N����N�ڶԳ�����Ҳࣩ������N��NH��x�ᣬ����ΪH����BD�ڵ�F����P���߶�OC��һ���㣬��MNȡ�����ֵʱ����HF+FP+![]() PC����Сֵ��
PC����Сֵ��
��2���ڣ�1���У���MNȡ�����ֵHF+FP+1/3PCȡ��Сֵʱ���ѵ�P����ƽ�Ƹ�![]() ��λ�õ���Q������AQ���ѡ�AOQ�Ƶ�Oƿʱ����תһ���ĽǶ�
��λ�õ���Q������AQ���ѡ�AOQ�Ƶ�Oƿʱ����תһ���ĽǶ�![]() ��0��<
��0��<![]() <360�㣩���õ���AOQ�����б�AQ���������ڵ�C����ת�����У��Ƿ����һ��Gʹ��
<360�㣩���õ���AOQ�����б�AQ���������ڵ�C����ת�����У��Ƿ����һ��Gʹ��![]() �������ڣ���ֱ��д���������������ĵ�Q�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ���ֱ��д���������������ĵ�Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
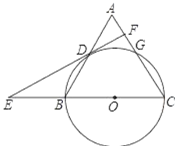
����Ŀ����ͼ������ABC�У�CA=CB=10��AB=12����BCΪֱ����Բ��O��AC�ڵ�G����AB�ڵ�D������D����O�����ߣ���CB���ӳ����ڵ�E����AC�ڵ�F�������н��ۣ���DF��AC����DO=DB����cos��E=![]() ����ȷ����__.
����ȷ����__.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ�ΰ�����ѧ�����������Σ����˳�ֱ��������Ϊ�����Σ��ָ��һ�������κ�����ȫ�ȵ�ֱ�������Σ����˽������ַָ�����õ�ͼ��֤���˹��ɶ�������ͼ��ʾ��a��3��b��4����������ε����Ϊ��������
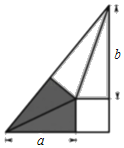
A. 10B. 12C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ŀڴ���װ���ĸ��ֱ����1��2��3��4��С�����ǵ���״����С����ȫ��ͬ.С���ȴӿڴ���������Żص�ȡ��һ��С��������Ϊx��С����ʣ��������С�������ȡ��һ��С��������y.
(1)������x��yȷ���ĵ�(x��y)�ں���![]() ͼ���ϵĸ��ʣ�
ͼ���ϵĸ��ʣ�
(2)С�ڡ�С��Լ����һ����Ϸ��������ǣ���x��y����xy>6����С��ʤ����x��y����xy<6,��С��ʤ.�����Ϸ����ƽ��?˵������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com