练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．一个多边形的每个内角都等于120°，则此多边形是（　　）
    A．五边形B．六边形C．七边形D．八边形

    分析 先求出这个多边形的每一个外角的度数，然后根据任意多边形外角和等于360°，再用360°除即可得到边数．

    解答 解：∵多边形的每一个内角都等于120°，
    ∴多边形的每一个外角都等于180°-120°=60°，
    ∴边数n=360°÷60°=6．
    故选：B．

    点评 此题主要考查了多边形的内角与外角的关系，求出每一个外角的度数是解答本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    14．若max{S1，S2，…，Sn}表示实数S1，S2，…，Sn中的最大者．设A=（a1，a2，a3），B=$（\begin{array}{l}{b1}\\{b2}\\{b3}\end{array}）$，记A?B=max{a1b1，a2b2，a3b3}，设A=（x+1，$\frac{1}{2x}$，1），B=$（\begin{array}{l}{1}\\{4x^2-2x}\\{|x+1|}\end{array}）$，若A?B=x+1，则x的取值范围为-1≤x≤2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．正比例函数y=kx与反比例函数$y=\frac{m}{x}$图象的一个交点坐标是（3，2），则m-3k=4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．某数学兴趣小组对线段上的动点问题进行探究，已知AB=8．
    问题思考：如图1，点P为线段AB上的一个动点，分别以AP、BP为边在同侧作正方形APDC与正方形PBFE．
    （1）在点P运动时，这两个正方形面积之和是定值吗？如果时求出；若不是，求出这两个正方形面积之和的最小值．
    （2）分别连接AD、DF、AF，AF交DP于点K，当点P运动时，在△APK、△ADK、△DFK中，是否存在两个面积始终相等的三角形？请说明理由．
    问题拓展：
    （3）如图2，以AB为边作正方形ABCD，动点P、Q在正方形ABCD的边上运动，且PQ=8．若点P从点A出发，沿A→B→C→D的线路，向D点运动，求点P从A到D的运动过程中，PQ的中点O所经过的路径的长．

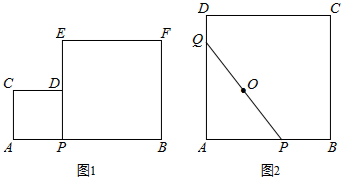
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列调查中，适宜采用普查方式的是（　　）
    A．调查市场上酸奶的质量情况
    B．调查某品牌圆珠笔芯的使用寿命
    C．调查乘坐飞机的旅客是否携带了危禁物品
    D．调查《最强大脑》节目的收视率情况

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．如图，三角形DEF是由ABC平移得到的．如果AB=4cm，AC=3cm，EF=5cm，那么三角形DEF的周长是12cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．在以下现象中，属于平移的是（　　）
    ①在挡秋千的小朋友；　       ②水平传送带上的物体
    ③宇宙中行星的运动         　 ④打气筒打气时，活塞的运动．
    A．①②B．③④C．②③D．②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

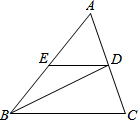    18．如图，在△ABC中，BD交AC于点D，DE交AB于点E，∠EBD=∠EDB，∠ABC：∠A：∠C=5：6：7，∠BDC=85°．
    （1）求∠BED的度数；
    （2）ED与BC有怎样的位置关系？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．综合实践
    （1）如图①，已知点P为等边△ABC外接圆的劣弧BC上任意一点，求证：
    PB+PC=PA．（提示：在PA上截取PM=PC，再证AM=PB ）
    （2）根据（1）的结论，在△ABC（其中∠A、∠B、∠C均小于120°）内部找一点P，使PA+PB+PC的值最小．作出这一点，并说明理由．
    （3）已知三个村庄A、B、C构成了如图③所示的△ABC（其中∠A、∠B、∠C均小于120°），AB=15km，BC=20km，∠B=30°，现选取一点P打水井，使水井P到三个村庄A、B、C所铺设的输水管总长度最小，求输水管总长度的最小值．

    查看答案和解析>>

    同步练习册答案