
【题目】如图,在等边三角形ABC中,BC=6cm.射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s). 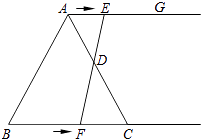
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)填空: ①当t为s时,四边形ACFE是菱形;
②当t为s时,以A、F、C、E为顶点的四边形是直角梯形.
【答案】
(1)证明:∵AG∥BC,
∴∠EAD=∠DCF,∠AED=∠DFC,
∵D为AC的中点,
∴AD=CD,
∵在△ADE和△CDF中,
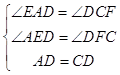 ,
,
∴△ADE≌△CDF(AAS)
(2)6;1.5
【解析】(2)解:①若四边形ACFE是菱形,则有CF=AC=AE=6, 则此时的时间t=6÷1=6(s);②四边形AFCE为直角梯形时,
(i)若CE⊥AG,则AE=3,BF=3×2=6,即点F与点C重合,不是直角梯形.
(ii)若AF⊥BC,
∵△ABC为等边三角形,
∴F为BC中点,即BF=3,
∴此时的时间为3÷2=1.5(s);
所以答案是:6;1.5.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°,以及对菱形的判定方法的理解,了解任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.


科目:初中数学 来源: 题型:
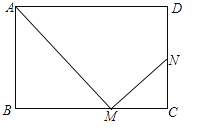
【题目】在矩形ABCD中,AB=a,AD=b,点M为BC边上一动点(点M与点B、C不重合),连接AM,过点M作MN⊥AM,垂足为M,MN交CD或CD的延长线于点N.
(1)求证:△CMN∽△BAM;
(2)设BM=x,CN=y,求y关于x的函数解析式.当x取何值时,y有最大值,并求出y的最大值;
(3)当点M在BC上运动时,求使得下列两个条件都成立的b的取值范围:①点N始终在线段CD上,②点M在某一位置时,点N恰好与点D重合.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两地有公路和铁路相连,在这条路上有一家食品厂,它到B地的距离是到A地的2倍,这家工厂从A地购买原料,制成食品卖到B地.已知公路运价为1.5元/(公里吨),铁路运价为1元/(公里吨),这两次运输(第一次:A地→食品厂,第二次:食品厂→B地)共支出公路运费15600元,铁路运费20600元.![]()
问:
(1)这家食品厂到A地的距离是多少?
(2)这家食品厂此次共买进原料和卖出食品各多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在给定的一张平行四边形纸片上作一个菱形,甲、乙两人的作法如下: 甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠BAD,∠ABC的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法请分别做出判断,并证明.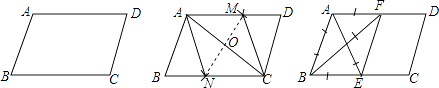
查看答案和解析>>
科目:初中数学 来源: 题型:
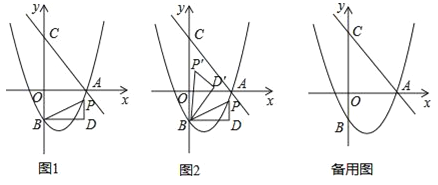
【题目】如图1,直线![]() 交x轴于点A,交y轴于点C(0,4),抛物线
交x轴于点A,交y轴于点C(0,4),抛物线![]() 经过点A,交y轴于点B(0,﹣2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为m.
经过点A,交y轴于点B(0,﹣2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为m.
(1)求抛物线的解析式;
(2)当△BDP为等腰直角三角形时,求线段PD的长;
(3)如图2,将△BDP绕点B逆时针旋转,得到△BD′P′,且旋转角∠PBP′=∠OAC,当点P的对应点P′落在坐标轴上时,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com