
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§÷±œΏ![]() ΫΜx÷α”ΎΒψAΘ§ΫΜy÷α”ΎΒψCΘ®0Θ§4Θ©Θ§≈ΉΈοœΏ
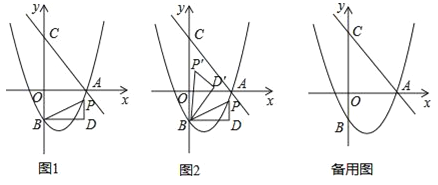
ΫΜx÷α”ΎΒψAΘ§ΫΜy÷α”ΎΒψCΘ®0Θ§4Θ©Θ§≈ΉΈοœΏ![]() Ψ≠ΙΐΒψAΘ§ΫΜy÷α”ΎΒψBΘ®0Θ§©¹2Θ©Θ°ΒψPΈΣ≈ΉΈοœΏ…œ“ΜΗωΕ·ΒψΘ§ΙΐΒψPΉςx÷αΒΡ¥ΙœΏPDΘ§ΙΐΒψBΉςBDΓΆPD”ΎΒψDΘ§Ν§Ϋ”PBΘ§…ηΒψPΒΡΚαΉχ±ξΈΣmΘ°
Ψ≠ΙΐΒψAΘ§ΫΜy÷α”ΎΒψBΘ®0Θ§©¹2Θ©Θ°ΒψPΈΣ≈ΉΈοœΏ…œ“ΜΗωΕ·ΒψΘ§ΙΐΒψPΉςx÷αΒΡ¥ΙœΏPDΘ§ΙΐΒψBΉςBDΓΆPD”ΎΒψDΘ§Ν§Ϋ”PBΘ§…ηΒψPΒΡΚαΉχ±ξΈΣmΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©Β±ΓςBDPΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ ±Θ§«σœΏΕΈPDΒΡ≥ΛΘΜ
Θ®3Θ©»γΆΦ2Θ§ΫΪΓςBDP»ΤΒψBΡφ ±’κ–ΐΉΣΘ§ΒΟΒΫΓςBDΓδPΓδΘ§«“–ΐΉΣΫ«ΓœPBPΓδ=ΓœOACΘ§Β±ΒψPΒΡΕ‘”ΠΒψPΓδ¬δ‘ΎΉχ±ξ÷α…œ ±Θ§«κ÷±Ϋ”–¥≥ωΒψPΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©PD=
ΘΜΘ®2Θ©PD=![]() ΜρPD=
ΜρPD=![]() ΘΜΘ®3Θ©PΘ®©¹
ΘΜΘ®3Θ©PΘ®©¹![]() Θ§
Θ§![]() Θ©ΜρPΘ®
Θ©ΜρPΘ®![]() Θ§
Θ§![]() Θ©ΜρPΘ®
Θ©ΜρPΘ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚΘ®1Θ©œ»»ΖΕ®≥ωΒψAΒΡΉχ±ξΘ§‘Ό”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ω≈ΉΈοœΏΫβΈω ΫΘΜ
Θ®2Θ©”…ΓςBDPΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§≈–Εœ≥ωBD=PDΘ§Ϋ®ΝΔmΒΡΖΫ≥ΧΦΤΥψ≥ωmΘ§¥”Εχ«σ≥ωPDΘΜ
Θ®3Θ©Ζ÷ΒψPΓδ¬δ‘Ύx÷αΚΆy÷αΝΫ÷÷«ιΩωΦΤΥψΦ¥Ω…Θ°
‘ΧβΫβΈωΘΚΘ®1Θ©ΓΏΒψCΘ®0Θ§4Θ©‘Ύ÷±œΏ![]() …œΘ§Γύn=4Θ§Γύ
…œΘ§Γύn=4Θ§Γύ![]() Θ§Ννy=0Θ§Γύx=3Θ§ΓύAΘ®3Θ§0Θ©Θ§ΓΏ≈ΉΈοœΏ
Θ§Ννy=0Θ§Γύx=3Θ§ΓύAΘ®3Θ§0Θ©Θ§ΓΏ≈ΉΈοœΏ![]() Ψ≠ΙΐΒψAΘ§ΫΜy÷α”ΎΒψBΘ®0Θ§©¹2Θ©Θ§Γύc=©¹2Θ§6+3b©¹2=0Θ§Γύb=
Ψ≠ΙΐΒψAΘ§ΫΜy÷α”ΎΒψBΘ®0Θ§©¹2Θ©Θ§Γύc=©¹2Θ§6+3b©¹2=0Θ§Γύb=![]() Θ§Γύ≈ΉΈοœΏΫβΈω ΫΈΣ
Θ§Γύ≈ΉΈοœΏΫβΈω ΫΈΣ![]() ΘΜ
ΘΜ
Θ®2Θ©ΒψPΈΣ≈ΉΈοœΏ…œ“ΜΗωΕ·ΒψΘ§…ηΒψPΒΡΚαΉχ±ξΈΣmΘ§ΓύPΘ®mΘ§![]() Θ©Θ§ΓύBD=|m|Θ§PD=
Θ©Θ§ΓύBD=|m|Θ§PD=![]() =
=![]() Θ§ΓΏΓςBDPΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§«“PDΓΆBDΘ§ΓύBD=PDΘ§Γύ|m|=
Θ§ΓΏΓςBDPΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§«“PDΓΆBDΘ§ΓύBD=PDΘ§Γύ|m|=![]() Θ§Γύm=0Θ®…αΘ©Θ§m=
Θ§Γύm=0Θ®…αΘ©Θ§m=![]() Θ§m=
Θ§m=![]() Θ§ΓύPD=
Θ§ΓύPD=![]() ΜρPD=
ΜρPD=![]() ΘΜ
ΘΜ
Θ®3Θ©ΓΏΓœPBP'=ΓœOACΘ§OA=3Θ§OC=4Θ§ΓύAC=5Θ§ΓύsinΓœPBP'=![]() Θ§cosΓœPBP'=
Θ§cosΓœPBP'=![]() Θ§Ζ÷ΝΫ÷÷«ιΩωΧ÷¬έΘΚ
Θ§Ζ÷ΝΫ÷÷«ιΩωΧ÷¬έΘΚ
ΔΌΒ±ΒψP'¬δ‘Ύx÷α…œ ±Θ§ΙΐΒψD'ΉςD'NΓΆx÷αΘ§¥ΙΉψΈΣNΘ§ΫΜBD”ΎΒψMΘ§ΓœDBD'=ΓœND'P'=ΓœPBP'Θ§»γΆΦ1Θ§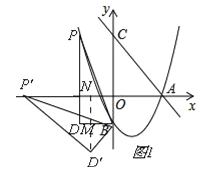
ND'©¹MD'=2Θ§Γύ![]() Θ§Γύm=
Θ§Γύm=![]() Θ®…αΘ©Θ§Μρm=©¹
Θ®…αΘ©Θ§Μρm=©¹![]() ΘΜ
ΘΜ
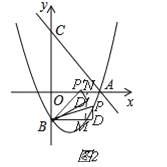
»γΆΦ2Θ§ ND'+MD'=2Θ§Γύ![]() Θ§Γύm=
Θ§Γύm=![]() Θ§Μρm=©¹
Θ§Μρm=©¹![]() Θ®…αΘ©Θ§ΓύPΘ®©¹
Θ®…αΘ©Θ§ΓύPΘ®©¹![]() Θ§
Θ§![]() Θ©ΜρPΘ®
Θ©ΜρPΘ®![]() Θ§
Θ§![]() Θ©ΘΜ
Θ©ΘΜ
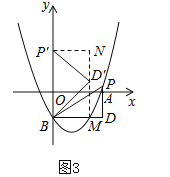
ΔΎΒ±ΒψP'¬δ‘Ύy÷α…œ ±Θ§»γΆΦ3Θ§ΙΐΒψDΓδΉςDΓδMΓΆx÷αΘ§ΫΜBD”ΎMΘ§ΙΐPΓδΉςPΓδNΓΆy÷αΘ§ΓύΓœDBDΓδ=ΓœNDΓδPΓδ=ΓœPBPΓδΘ§ΓΏPΓδN=BMΘ§Γύ![]() Θ§Γύm=
Θ§Γύm=![]() Θ§ΓύPΘ®
Θ§ΓύPΘ®![]() Θ§
Θ§![]() Θ©ΘΜ
Θ©ΘΜ
Ήέ…œΥυ ωΘΚPΘ®©¹![]() Θ§
Θ§![]() Θ©ΜρPΘ®
Θ©ΜρPΘ®![]() Θ§
Θ§![]() Θ©ΜρPΘ®
Θ©ΜρPΘ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°


 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΒ»±Ώ»ΐΫ«–ΈABC÷–Θ§BC=6cmΘ°…δœΏAGΓΈBCΘ§ΒψE¥”ΒψA≥ωΖΔ―Ί…δœΏAG“‘1cm/sΒΡΥΌΕ»‘ΥΕ·Θ§Ά§ ±ΒψF¥”ΒψB≥ωΖΔ―Ί…δœΏBC“‘2cm/sΒΡΥΌΕ»‘ΥΕ·Θ§…η‘ΥΕ· ±ΦδΈΣtΘ®sΘ©Θ° 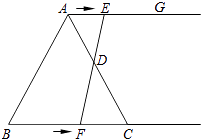
Θ®1Θ©Ν§Ϋ”EFΘ§Β±EFΨ≠ΙΐAC±ΏΒΡ÷–ΒψD ±Θ§«σ÷ΛΘΚΓςADEΓ’ΓςCDFΘΜ
Θ®2Θ©ΧνΩ’ΘΚ ΔΌΒ±tΈΣs ±Θ§ΥΡ±Ώ–ΈACFE «Νβ–ΈΘΜ
ΔΎΒ±tΈΣs ±Θ§“‘AΓΔFΓΔCΓΔEΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «÷±Ϋ«Χί–ΈΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫΆ§―ßΒΡΦ“”κ―ß–ΘΒΡΨύάκΨυΈΣ3000ΟΉΘ°ΦΉΆ§―ßœ»≤Ϋ––600ΟΉΘ§»ΜΚσ≥ΥΙΪΫΜ≥Β»Ξ―ß–ΘΓΔ““Ά§―ßΤοΉ‘––≥Β»Ξ―ß–ΘΘ°“―÷ΣΦΉ≤Ϋ––ΥΌΕ» «““ΤοΉ‘––≥ΒΥΌΕ»ΒΡ ![]() Θ§ΙΪΫΜ≥ΒΒΡΥΌΕ» «““ΤοΉ‘––≥ΒΥΌΕ»ΒΡ2±ΕΘ°ΦΉ““ΝΫΆ§―ßΆ§ ±¥”Φ“ΖΔ»Ξ―ß–ΘΘ§ΫαΙϊΦΉΆ§―ß±»““Ά§―ß‘γΒΫ2Ζ÷÷”Θ°
Θ§ΙΪΫΜ≥ΒΒΡΥΌΕ» «““ΤοΉ‘––≥ΒΥΌΕ»ΒΡ2±ΕΘ°ΦΉ““ΝΫΆ§―ßΆ§ ±¥”Φ“ΖΔ»Ξ―ß–ΘΘ§ΫαΙϊΦΉΆ§―ß±»““Ά§―ß‘γΒΫ2Ζ÷÷”Θ°
Θ®1Θ©«σ““ΤοΉ‘––≥ΒΒΡΥΌΕ»ΘΜ
Θ®2Θ©Β±ΦΉΒΫ¥ο―ß–Θ ±Θ§““Ά§―ßάκ―ß–ΘΜΙ”–Εύ‘ΕΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–Έ÷ΫΤ§ABCD÷–Θ§“―÷ΣAD=8Θ§’έΒΰ÷ΫΤ§Θ§ ΙAB±Ώ”κΕ‘Ϋ«œΏAC÷ΊΚœΘ§ΒψB¬δ‘ΎΒψF¥ΠΘ§’έΚέΈΣAEΘ§«“EF=3Θ§‘ρABΒΡ≥ΛΈΣΘ® Θ©
A.3
B.4
C.5
D.6
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΨΊ–Έ÷ΫΤ§ABCD÷–Θ§ΒψE «ADΒΡ÷–ΒψΘ§«“AE=1Θ§BEΒΡ¥Ι÷±ΤΫΖ÷œΏMN«ΓΚΟΙΐΒψCΘ°‘ρΨΊ–ΈΒΡ“Μ±ΏABΒΡ≥ΛΕ»ΈΣΘ® Θ© 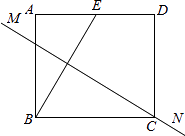
A.1
B.![]()
C.![]()
D.2
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§–ΓœΆΈΣΝΥΧε―ιΥΡ±Ώ–ΈΒΡ≤ΜΈ»Ε®–‘Θ§ΫΪΥΡΗυΡΨΧθ”ΟΕΛΉ”ΕΛ≥…“ΜΗωΨΊ–ΈΩρΦήABCDΘ§B”κDΝΫΒψ÷°Φδ”Ο“ΜΗυœπΤΛΫνά≠÷±ΙΧΕ®Θ§»ΜΚσœρ”“≈ΛΕ·ΩρΦήΘ§Ιέ≤λΥυΒΟΥΡ±Ώ–ΈΒΡ±δΜ·Θ§œ¬Ν–≈–Εœ¥μΈσΒΡ «Θ® Θ© 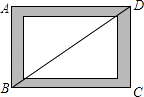
A.ΥΡ±Ώ–ΈABCD”…ΨΊ–Έ±δΈΣΤΫ––ΥΡ±Ώ–Έ
B.BDΒΡ≥ΛΕ»‘ω¥σ
C.ΥΡ±Ώ–ΈABCDΒΡΟφΜΐ≤Μ±δ
D.ΥΡ±Ώ–ΈABCDΒΡ÷ή≥Λ≤Μ±δ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–≈–Εœ÷–Θ§≤Μ’ΐ»ΖΒΡ”–Θ®ΓΓΓΓΘ©
A.»ΐ±ΏΕ‘”Π≥…±»άΐΒΡΝΫΗω»ΐΫ«–ΈœύΥΤ
B.ΝΫ±ΏΕ‘”Π≥…±»άΐΘ§«“”–“ΜΗωΫ«œύΒ»ΒΡΝΫΗω»ΐΫ«–ΈœύΥΤ
C.–±±Ώ”κ“ΜΧθ÷±Ϋ«±ΏΕ‘”Π≥…±»άΐΒΡΝΫΗω÷±Ϋ«»ΐΫ«–ΈœύΥΤ
D.”–“ΜΗωΫ« «100ΓψΒΡΝΫΗωΒ»―ϋ»ΐΫ«–ΈœύΥΤ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§‘ΎΓςABO÷–Θ§ΓœOAB=90ΓψΘ§ΓœAOB=30ΓψΘ§OB=8Θ°“‘OBΈΣ“Μ±ΏΘ§‘ΎΓςOABΆβΉςΒ»±Ώ»ΐΫ«–ΈOBCΘ§D «OBΒΡ÷–ΒψΘ§Ν§Ϋ”AD≤Δ―”≥ΛΫΜOC”ΎEΘ°
Θ®1Θ©«σΒψBΒΡΉχ±ξΘΜ
Θ®2Θ©«σ÷ΛΘΚΥΡ±Ώ–ΈABCE «ΤΫ––ΥΡ±Ώ–ΈΘΜ
Θ®3Θ©»γΆΦ2Θ§ΫΪΆΦ1÷–ΒΡΥΡ±Ώ–ΈABCO’έΒΰΘ§ ΙΒψC”κΒψA÷ΊΚœΘ§’έΚέΈΣFGΘ§«σOGΒΡ≥ΛΘ°
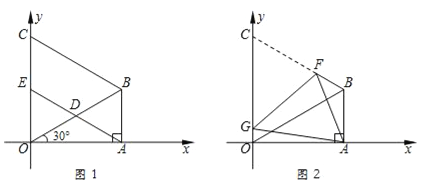
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ»ΐΫ«–ΈΒΡΝΫ±ΏΖ÷±πΈΣ3ΚΆ7Θ§‘ρ¥Υ»ΐΫ«–ΈΒΡΒΎ»ΐ±ΏΩ…Ρή «Θ® Θ©
A. 3 B. 4 C. 5 D. 10
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com